 είναι δύο γραμμικά ανεξάρτητες λύσεις της εξίσωσης
είναι δύο γραμμικά ανεξάρτητες λύσεις της εξίσωσης  όπου
όπου  (διάστημα) και
(διάστημα) και  συνεχείς συναρτήσεις στο
συνεχείς συναρτήσεις στο  να αποδείξετε ότι μεταξύ δύο διαδοχικών λύσεων της
να αποδείξετε ότι μεταξύ δύο διαδοχικών λύσεων της  υπάρχει λύση της
υπάρχει λύση της 
Συντονιστής: Πρωτοπαπάς Λευτέρης
 είναι δύο γραμμικά ανεξάρτητες λύσεις της εξίσωσης
είναι δύο γραμμικά ανεξάρτητες λύσεις της εξίσωσης  όπου
όπου  (διάστημα) και
(διάστημα) και  συνεχείς συναρτήσεις στο
συνεχείς συναρτήσεις στο  να αποδείξετε ότι μεταξύ δύο διαδοχικών λύσεων της
να αποδείξετε ότι μεταξύ δύο διαδοχικών λύσεων της  υπάρχει λύση της
υπάρχει λύση της 
Είναι γνωστή πρόταση (νομίζω ονομάζεται Θεώρημα Sturm), και υπάρχει σε όλα τα βιβλία Διαφορικών Εξισώσεων αλλά ίσως με χρήση ελαφριά εξωσχολικών εργαλείων. Ας την δούμε συνοπτικά με σχολικά εργαλεία (ουσιαστικά επαναλαμβάνω γνωστά θέματα με μικρές προσαρμογές), με την προσθήκη ότι στην εξωσχολική φράση "γραμμικά ανεξάρτητες" θα εννοούμε "όχι η μία πολλαπλάσιο της άλλης, σε οποιοδήποτε διάστημα" (προσοχή, αυτό είναι ισχυρότερο από την γραμμική ανεξαρτησία).Πρωτοπαπάς Λευτέρης έγραψε: ↑Σάβ Φεβ 04, 2023 5:10 pmΑνείναι δύο γραμμικά ανεξάρτητες λύσεις της εξίσωσης
όπου
(διάστημα) και
συνεχείς συναρτήσεις στο
να αποδείξετε ότι μεταξύ δύο διαδοχικών λύσεων της
υπάρχει λύση της

 δύο τέτοιες λύσεις, δηλαδή
δύο τέτοιες λύσεις, δηλαδή  . Πολλαπλασιάζουμε την πρώτη επί
. Πολλαπλασιάζουμε την πρώτη επί  και την δεύτερη επί
και την δεύτερη επί  και αφαιρούμε. Δίνει
και αφαιρούμε. Δίνει  ή αλλιώς
ή αλλιώς  . Δηλαδή της μορφής
. Δηλαδή της μορφής  . Στο επόμενο βήμα τα βιβλία συνήθως προχωρούν με "ολοκληρωτικό παράγοντα" αλλά το διαμορφώνω σε σχολικά Μαθηματικά. Αν
. Στο επόμενο βήμα τα βιβλία συνήθως προχωρούν με "ολοκληρωτικό παράγοντα" αλλά το διαμορφώνω σε σχολικά Μαθηματικά. Αν  αρχική της
αρχική της  τότε η προηγούμενη γράφεται
τότε η προηγούμενη γράφεται  , δηλαδή
, δηλαδή  , οπότε γιά κάποια σταθερά
, οπότε γιά κάποια σταθερά  είναι
είναι 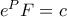 ή αλλιώς
ή αλλιώς 
 δύο διαδοχικές ρίζες της
δύο διαδοχικές ρίζες της  . Έστω ακόμη (για να πάμε σε άτοπο) ότι η
. Έστω ακόμη (για να πάμε σε άτοπο) ότι η  δεν μηδενίζεται στο μεσοδιάστημα
δεν μηδενίζεται στο μεσοδιάστημα  .
. στην
στην  είναι μη μηδενική γιατί αλλιώς στο
είναι μη μηδενική γιατί αλλιώς στο  θα είχαμε ότι ορίζεται η
θα είχαμε ότι ορίζεται η  και ότι
και ότι 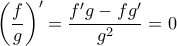 . Άρα
. Άρα  για κάποια σταθερά
για κάποια σταθερά  , άτοπο (από την ελαφριά ενισχυμένη υπόθεση περί γραμμικής ανεξαρτησίας).
, άτοπο (από την ελαφριά ενισχυμένη υπόθεση περί γραμμικής ανεξαρτησίας).  έχουμε ότι το δεξί μέλος της
έχουμε ότι το δεξί μέλος της  δεν μηδενίζεται πουθενά (ιδιότητα της εκθετικής). Έπεται ότι
δεν μηδενίζεται πουθενά (ιδιότητα της εκθετικής). Έπεται ότι  γιατί αλλιώς η (*) θα έδινε
γιατί αλλιώς η (*) θα έδινε  δεδομένου ότι
δεδομένου ότι  . Όμοια
. Όμοια 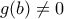 . Άρα η
. Άρα η  ορίζεται και στα άκρα του
ορίζεται και στα άκρα του  .
.  στο
στο ![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) (εδώ γίνεται χρήση της
(εδώ γίνεται χρήση της  ). Έπεται ότι υπάρχει
). Έπεται ότι υπάρχει  όπου μηδενίζεται η παράγωγός της, οπότε ισχύει
όπου μηδενίζεται η παράγωγός της, οπότε ισχύει  , και άρα
, και άρα  . Άτοπο στην
. Άτοπο στην  αφού
αφού  . Τελειώσαμε.
. Τελειώσαμε.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες