 , έχει δύο ακριβώς ρίζες
, έχει δύο ακριβώς ρίζες  .
.Δείξτε ότι γι αυτές τις ρίζες , ισχύει :
 .
.Συντονιστής: Γιώργος Ρίζος
 , έχει δύο ακριβώς ρίζες
, έχει δύο ακριβώς ρίζες  .
. .
. , με
, με  τέτοια, ώστε
τέτοια, ώστε και
και  , είναι
, είναι 

![[xlnx-x]_{x_{1}}^{x_{2}} > [x-lnx]_{x_{1}}^{x_{2}} \Rightarrow [xlnx-x]_{x_{1}}^{x_{2}} > [x-lnx]_{x_{1}}^{x_{2}} \Rightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/1b9f922f135c9df50c75a4917756e1aa.png)




 Στην λύση του , ο Λάμπρος χρησιμοποίησε την "γνωστή" :
Στην λύση του , ο Λάμπρος χρησιμοποίησε την "γνωστή" :  .
. για κάθε
για κάθε 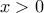 τότε
τότε το
το  , έχουμε αμέσως
, έχουμε αμέσως  ,
,


 , ισχύει η ισότητα.
, ισχύει η ισότητα.

 εμφανίζει ολικό ελάχιστο για
εμφανίζει ολικό ελάχιστο για 
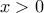 ισχύει ότι
ισχύει ότι 
 , για
, για  .
. :
:  .
. :
:  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες