Ο καημός του θεματοδότη
Δημοσιεύτηκε: Σάβ Ιαν 12, 2019 9:13 am
Στο ορθογώνιο τρίγωνο  , είναι :
, είναι :  . Στην πλευρά
. Στην πλευρά  θεωρούμε
θεωρούμε
σημείο , έτσι ώστε :
, έτσι ώστε :  . Δεν είναι απαραίτητο να απαντήσετε σε όλα τα παρακάτω ερωτήματα .
. Δεν είναι απαραίτητο να απαντήσετε σε όλα τα παρακάτω ερωτήματα .
α) Σχεδιάστε κύκλο διερχόμενο από τα και εφαπτόμενο της
και εφαπτόμενο της  . Υπολογίστε την ακτίνα του .
. Υπολογίστε την ακτίνα του .
β) Βρείτε εκείνη τη θέση του , για την οποία ο κύκλος αυτός έχει την ελάχιστη ακτίνα .
, για την οποία ο κύκλος αυτός έχει την ελάχιστη ακτίνα .
γ) Αν ο κύκλος τέμνει την στο
στο  , για ποια θέση του
, για ποια θέση του  προκύπτει :
προκύπτει :  ;
;
Σύγχρονη τεχνολογική βοήθεια επιτρεπτή
 , είναι :
, είναι :  . Στην πλευρά
. Στην πλευρά  θεωρούμε
θεωρούμε σημείο
 , έτσι ώστε :
, έτσι ώστε :  . Δεν είναι απαραίτητο να απαντήσετε σε όλα τα παρακάτω ερωτήματα .
. Δεν είναι απαραίτητο να απαντήσετε σε όλα τα παρακάτω ερωτήματα .α) Σχεδιάστε κύκλο διερχόμενο από τα
 και εφαπτόμενο της
και εφαπτόμενο της  . Υπολογίστε την ακτίνα του .
. Υπολογίστε την ακτίνα του .β) Βρείτε εκείνη τη θέση του
 , για την οποία ο κύκλος αυτός έχει την ελάχιστη ακτίνα .
, για την οποία ο κύκλος αυτός έχει την ελάχιστη ακτίνα .γ) Αν ο κύκλος τέμνει την
 στο
στο  , για ποια θέση του
, για ποια θέση του  προκύπτει :
προκύπτει :  ;
;Σύγχρονη τεχνολογική βοήθεια επιτρεπτή
 και φέρνω σε αυτόν το εφαπτόμενο τμήμα
και φέρνω σε αυτόν το εφαπτόμενο τμήμα  Στη συνέχεια
Στη συνέχεια που τέμνει την
που τέμνει την 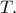 Ο περίκυκλος του
Ο περίκυκλος του  είναι ο ζητούμενος κύκλος.
είναι ο ζητούμενος κύκλος.

 και
και 
 και με Πυθαγόρειο στο
και με Πυθαγόρειο στο 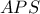 όπου
όπου  παίρνω:
παίρνω:
 άρα έχουμε ελάχιστη ακτίνα όταν τα σημεία
άρα έχουμε ελάχιστη ακτίνα όταν τα σημεία  είναι συνευθειακά, δηλαδή το
είναι συνευθειακά, δηλαδή το  είναι ύψος του τριγώνου.
είναι ύψος του τριγώνου.  απ' όπου παίρνω
απ' όπου παίρνω  και
και 
 και αντκαθιστώντας στον γενικό τύπο
και αντκαθιστώντας στον γενικό τύπο 