 ημικυκλίου , κινείται σημείο
ημικυκλίου , κινείται σημείο  και έστω
και έστω 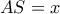 . Γράφουμε το ημικύκλιο
. Γράφουμε το ημικύκλιοδιαμέτρου
 , προς το οποίο φέρουμε το εφαπτόμενο τμήμα
, προς το οποίο φέρουμε το εφαπτόμενο τμήμα  . Υπολογίστε το :
. Υπολογίστε το : 
Αν
 , δοκιμάστε να βρείτε το
, δοκιμάστε να βρείτε το  , με χρήση του Wolframalpha και ... σχολιάστε !
, με χρήση του Wolframalpha και ... σχολιάστε !Συντονιστής: Γιώργος Ρίζος
 ημικυκλίου , κινείται σημείο
ημικυκλίου , κινείται σημείο  και έστω
και έστω 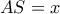 . Γράφουμε το ημικύκλιο
. Γράφουμε το ημικύκλιο , προς το οποίο φέρουμε το εφαπτόμενο τμήμα
, προς το οποίο φέρουμε το εφαπτόμενο τμήμα  . Υπολογίστε το :
. Υπολογίστε το : 
 , δοκιμάστε να βρείτε το
, δοκιμάστε να βρείτε το  , με χρήση του Wolframalpha και ... σχολιάστε !
, με χρήση του Wolframalpha και ... σχολιάστε ! , για
, για  .
. , ουσιαστικά ψάχνουμε πού μεγιστοποιείται η
, ουσιαστικά ψάχνουμε πού μεγιστοποιείται η  , για
, για  . Με παραγώγιση το μέγιστο είναι για
. Με παραγώγιση το μέγιστο είναι για  , και λοιπά.
, και λοιπά.Αν
 είναι η ακτίνα του μικρού ημικυκλίου, τότε
είναι η ακτίνα του μικρού ημικυκλίου, τότε  Όπως ο Μιχάλης,
Όπως ο Μιχάλης, 
 Άρα για
Άρα για 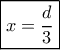 έχουμε
έχουμε 
 τότε
τότε  και
και 
Θεώρησα ως μεταβλητή τοgeorge visvikis έγραψε: ↑Κυρ Ιαν 19, 2020 10:36 am
Το ίδιο βγάζει και το Wolframalpha. Μάλλον κάτι άλλο έχεις στο μυαλό σου Θανάση .
 , οπότε :
, οπότε :  .
. μεγιστοποιείται για
μεγιστοποιείται για  και είναι :
και είναι :  .
. , παίρνουμε :
, παίρνουμε :  .
. , για την :
, για την : 
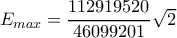 . Η εξήγηση είναι ότι το κλάσμα
. Η εξήγηση είναι ότι το κλάσμα 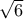 . Τώρα που το ξαναδοκιμάζω βγάζει το
. Τώρα που το ξαναδοκιμάζω βγάζει το  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Google [Bot] και 4 επισκέπτες