Είχε ο Ευκλείδης δίκιο;

[thanasis kopadis]

Ένας από τους λογίους που προσέλκυσε η Αλεξάνδρεια γύρω στο 300 π.Χ. ήταν κι ο Ευκλείδης, ο οποίος βρέθηκε εκεί για να ιδρύσει μια σχολή μαθηματικών. Ελάχιστα πράγματα γνωρίζουμε για τη ζωή του, φαίνεται όμως να εκπαιδεύτηκε στην Ακαδημία από μαθητές του Πλάτωνα. Αυτό που καθιέρωσε τον Ευκλείδη ως ένα από τα μεγαλύτερα ονόματα στην ιστορία των μαθηματικών ήταν η συγγραφή των Στοιχείων. Το έργο αυτό άσκησε βαθιά επίδραση στη δυτική σκέψη, καθώς μελετούνταν, αναλυόταν και εκδιδόταν επί αιώνες μέχρι και τα νεότερα χρόνια. Έχει λεχθεί ότι από όλα τα βιβλία του δυτικού πολιτισμού μόνο η Βίβλος μελετήθηκε πιο εξονυχιστικά από τα Στοιχεία του Ευκλείδη.

Τα Στοιχεία είναι μια τεράστια συλλογή 13 βιβλίων, αποτελούμενη από 465 προτάσεις σχετικά με τη γεωμετρία του επιπέδου, του χώρου, αλλά και τη θεωρία των αριθμών. Η μεγαλοφυία του Ευκλείδη δεν έγκειται τόσο στη δημιουργία νέων μαθηματικών όσο στην παρουσίαση των παλαιών μαθηματικών με έναν απολύτως σαφή, οργανωμένο και λογικό τρόπο, δίνοντας μας έτσι μια θαυμάσια αξιωματική ανάπτυξη του αντικειμένου του.

Στην αρχή των Στοιχείων παραθέτει λίγα βασικά πράγματα: 23 ορισμούς (π.χ. γραμμή είναι κάθετι που έχει μήκος χωρίς πλάτος), 5 αιτήματα (π.χ το αίτημα 1 που λέει ότι είναι δυνατόν να φέρουμε ευθεία γραμμή από κάθε σημείο προς οποιοδήποτε σημείο) και 5 γενικά αξιώματα (π.χ. μεγέθη που είναι ίσα προς τρίτο μέγεθος είναι και μεταξύ τους ίσα). Αυτά ήταν τα θεμέλια του συστήματός του. Μπορούσε να τα χρησιμοποιήσει όποια στιγμή επιθυμούσε. Από αυτά απέδειξε την πρώτη του πρόταση και στη συνέχεια κατάφερε να αναμείξει τους ορισμούς, τα αιτήματα, τα αξιώματα και την πρώτη του πρόταση ώστε να αποδείξει τη δεύτερη πρόταση . Και συνέχισε με αυτόν τον τρόπο.

Στο διάβα της ιστορίας όμως, ένα από τα αιτήματα των Στοιχείων και συγκεκριμένα το 5ο, αποτέλεσε το πιο προβληματικό χαρακτηριστικό του όλου συστήματος.
Το αίτημα 5 λέει ότι: αν μια ευθεία τέμνει δύο άλλες και σχηματίζει με αυτές ζεύγος γωνιών "εντός και επί τα αυτά" με άθροισμα μικρότερο των δύο ορθών, τότε οι ευθείες, αν προεκταθούν επ' άπειρον, τέμνονται προς το μέρος που βρίσκονται οι γωνίες αυτές.

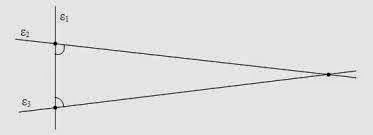
Το πρόβλημα δεν ανέκυψε επειδή κάποιος αμφισβήτησε ότι το αίτημα των παραλλήλων έπρεπε να είναι αληθές. Αντιθέτως, υπήρξε παγκόσμια συναίνεση ότι το αίτημα ήταν μια λογική αναγκαιότητα.

Σε τελική ανάλυση, η γεωμετρία ήταν ένας αφηρημένος τρόπος περιγραφής του σύμπαντος και η "φυσική" πραγματικότητα υπαγόρευσε την αλήθεια του αιτήματος αυτού. Αυτό που αμφισβητήθηκε ήταν η ταξινόμησή του στα αιτήματα. Ο κλασικός συγγραφέας Πρόκλος συνόψισε την άποψη αυτή με το παρακάτω σχόλιο: " Τούτο (το πέμπτο αίτημα) θα έπρεπε να διαγραφεί από τα αιτήματα, διότι πρόκειται για θεώρημα και μπορεί να αποδειχθεί..". Αυτή η πεποίθηση δεν προκάλεσε έκπληξη. Ακόμη και ο ίδιος ο Ευκλείδης έμοιαζε να αποφεύγει όσο μπορούσε τη χρήση του αιτήματος και κατάφερε να αποδείξει πολύπλοκα αποτελέσματα χωρίς αυτό.

Όλα αυτά αποτελούσαν πολύ καλό λόγο για να ξεκινήσει η αναζήτηση μιας απόδειξης του αιτήματος. Στην προσπάθεια αυτή οι μαθηματικοί ήταν ελεύθεροι να χρησιμοποιήσουν οποιοδήποτε από τα υπόλοιπα 4 αιτήματα, τα αξιώματα, αλλά και πάνω από 20 προτάσεις οι οποίες δε χρησιμοποιούσαν την υπό εξέταση δήλωση. Αναρίθμητοι μαθηματικοί δοκίμασαν τις ικανότητές τους στην επινόηση μιας απόδειξης. Δυστυχώς τα χρόνια της απογοήτευσης έγιναν δεκαετίες και κατόπιν αιώνες αποτυχίας.

Η απόδειξη συνέχιζε να διαφεύγει μέχρι την Αναγέννηση και καθ'όλη τη διάρκειά της. Όποιος αποδείκνυε το αίτημα των παραλλήλων θα εξασφάλιζε αιώνια φήμη στα χρονικά των μαθηματικών.

Τότε, στις αρχές του 19ου αιώνα, τρεις μαθηματικοί είχαν ταυτόχρονα εκείνη την έκλαμψη που ήταν αναγκαία για να δουν το πρόβλημα στις πραγματικές του διαστάσεις.

Ο πρώτος ήταν ο ασύγκριτος Καρλ Φρίντριχ Γκάους (1777-1855).
Ο Γκάους αναδιατύπωσε το πρόβλημα με βάση το άθροισμα των γωνιών ενός τριγώνου. Επιθυμώντας να αποδείξει ότι το άθροισμα των γωνιών ενός τριγώνου πρέπει να είναι ίσο με 180 μοίρες, υπέθεσε ότι αυτό δεν ισχύει. Κάνοντας χρήση του γεγονότος ότι οι ευθείες έχουν άπειρο μήκος (υπόθεση την οποία είχε κάνει και ο Ευκλείδης και κανεις ως τότε δεν είχε αμφισβητήσει) διαπίστωσε ότι η υπόθεση το άθροισμα των γωνιών ενός τριγώνου να υπερβαίνει τις 180 μοίρες οδηγούσε σε λογική αντίφαση. Έτσι, η περίπτωση αυτή απορριπτόταν.
΄Αν κατάφερνε με παρόμοιο τρόπο να απαλλαγεί και από τη δεύτερη περίπτωση, θα είχε θεμελιώσει έμμεσα την αναγκαιότητα του αιτήματος των παραλλήλων. Ξεκινώτας όμως από την υπόθεση ότι το άθροισμα των γωνιών ενός τριγώνου είναι μικρότερο από 180 μοίρες, ο Γκάους άρχισε να εξάγει συμπεράσματα παράξενα, φαινομενικά αλλόκοτα και αντίθετα στη διαίσθηση.
Ωστόσο δε βρήκε πουθενά τη λογική αντίφαση που αναζητούσε. Βαθμιαία, καθώς προχωρούσε ολοένα και βαθύτερα σε αυτή την παράξενη γεωμετρία άρχισε να αισθάνεται ότι ανέπτυσσε όχι μια μη συνεπή, αλλά μια εναλλακτική γεωμετρία, μια "μη ευκλείδεια" γεωμετρία όπως την αποκάλεσε ο ίδιος σε μια ιδιωτική επιστολή το 1824. Ήταν μια δήλωσε που έκοβε την ανάσα. Ο Γκάους όμως, ποτέ δε δημοσιοποίησε αυτά τα ευρήματά του. Ήταν βέβαιος πως η αμφιλεγόμενη φύση της άποψης του θα προκαλούσε θόρυβο που ενδεχομένως να έθετε σε κίνδυνο την υψηλή του φήμη.

Στη συνέχεια ήρθε στο προσκήνιο ο Ούγγρος μαθηματικός Γιάνος Μπόλιαϊ (1802-1860).
Ο πατέρας του, ο Φάρκας Μπόλιαϊ, υπήρξε συνεργάτης του Γκάους και είχε αφιερώσει μεγάλο μέρος της ζωής του σε μια μάταιη προσπάθεια να αποδείξει το αίτημα του Ευκλείδη.
"Σε εκλιπαρώ , άφησε ήσυχη την επιστήμη των παραλλήλων" είχε προειδοποιήσει τον γιό του, όμως ο νεαρός Γιάνος αγνόησε τη συμβουλή του πατέρα του. Σχεδόν όπως και ο Γκάους ενέσκηπτε ολοένα και βαθύτερα στο πρόβλημα, καταλήγοντας και αυτός στο συμπέρασμα ότι η γεωμετρία του Ευκλείδη είχε έναν λογικά έγκυρο ανταγωνιστή. "Από το τίποτα δημιούργησα ένα παράξενο σύμπαν" έγραψε με έκπληξη δίπλα στις φαινομενικά συνεπείς προτάσεις του. Ο ίδιος δημοσίευσε τα ευρήματά του το 1832. Ωστόσο, όταν έμαθε ότι η μεγαλύτερή του ανακάλυψη βρισκόταν επί δεκαετίες στο συρτάρι του Γκάους, ο εγωισμός του υπέστει ψυχρολουσία.

Ο εγωισμός του Γιάνος έμελλε να υποστεί ακόμη μια δοκιμασία καθώς σύντομα έγινε γνωστό ότι ο Ρώσος μαθηματικός Νικολάι Λομπατσέφσκυ (1793-1856) όχι μόνο είχε διατρέξει την ίδια διαδρομή, αλλά είχε δημοσιεύσει τη δική του θεώρηση της μη ευκλείδειας γεωμετρίας το 1829, δηλαδή τρία χρόνια νωρίτερα.
Ο Λομπατσέφσκυ όμως είχε γράψει την εργασία του στα ρώσικα, με αποτέλεσμα αυτή να περάσει απαρατήρητη στη δυτική Ευρώπη.

Ο αντίκτυπος αυτών των ανακαλύψεων είχε βρει τον στόχο του, όταν ακόμη ένας νεωτεριστής μαθηματικός, ο Μπέρνχαρτ Ρήμαν (1826-1866), υιοθέτησε μια διαφορετική θεώρηση σχετικά με το άπειρο μήκος γεωμετρικών γραμμών.
Όταν ο Ρήμαν επανεξέτασε τη γεωμετρία υποθέτοντας μη φραγμένες αλλά πεπερασμένες γραμμές, η αντίφαση που προέκυπτε από το γεγονός ότι το άθροισμα των γωνιών ενός τριγώνου ξεπερνούσε τις 180 μοίρες εξαφανίστηκε. Με αυτό τον τρόπο ο Ρήμαν ανέπτυξε ένα άλλο είδος μη ευκλείδειας γεωμετρίας, στο πλαίσιο της οποίας το άθροισμα των γωνιών ενός τριγώνου υπερβαίνει τις δύο ορθές. Μολονότι είναι διαφορετική τόσο από τη γεωμετρία του Ευκλείδη, όσο και από τη γεωμετρία των Γκάους και Μπόλιαϊ, η γεωμετρία του Ρήμαν είναι εξίσου συνεπής.

Σήμερα, αναγνωρίζουμε και τους τέσσερις μαθηματικούς ως δημιουργούς της μη ευκλείδειας γεωμετρίας.

Που βρίσκεται όμως ο Ευκλείδης μετά από αυτές τις ανακαλύψεις του 19ου αιώνα; H γεωμετρία του έπαψε να είναι η μόνη λογικά συνεπής περιγραφή του χώρου. Προς μεγάλη έκπληξη όλων, αποδείχθηκε ότι το αίτημα των παραλλήλων δεν προέκυπτε υποχρεωτικά από τη λογική. ΄Ηταν μια υπόθεση του Ευκλείδη, αλλά δεν υπήρχε καμία μαθηματική αναγκαιότητα για αυτό. Υπήρχαν ανταγωνιστικές εξίσου έγκυρες γεωμετρίες.
Το αποτέλεσμα όμως φαίνεται να είναι η ενίσχυση και όχι ο καταποντισμός της φήμης του Ευκλείδη. Και αυτό, γιατί αντίθετα με πολλούς που ακολούθησαν, ο Ευκλείδης δεν έπεσε στην παγίδα να προσπαθήσει να αποδείξει το αίτημα των παραλλήλων από τις υπόλοιπες αυταπόδεικτες αλήθειες, ένα εγχείρημα που, όπως γνωρίζουμε σήμερα, είναι καταδικασμένο να αποτύχει. Αντίθετα, τοποθέτησε απλώς την υπόθεσή του εκεί όπου άνηκε, στα αιτήματα.

Είκοσι δύο αιώνες αργότερα, οι μαθηματικοί απέδειξαν ότι ο Ευκλείδης είχε ανέκαθεν δίκιο.

Πηγή: Τα μεγάλα θεωρήματα των μαθηματικών, William Dunham. Εκδόσεις Αλεξάνδρεια

http://thanasiskopadis.blogspot.gr/2015 ... -post.html

[sokrazara]

Δηλαδή το ευκλείδειο αίτημα δεν αποδεικνύεται. εγώ πιστεύω πως στον ευκλείδειο χώρο (δηλαδή στο επίπεδο με μηδενική καμπυλότητα) το 5ο αίτημα αποδεικνύεται. Μάλιστα πιστεύω πως το έχω αποδείξει. Άλλωστε δεν υπάρχουν άλυτα προβλήματα αλλά πολύ δύσκολα στην απόδειξη προβλήματα.

[stranger]

Δηλαδή το ευκλείδειο αίτημα δεν αποδεικνύεται. εγώ πιστεύω πως στον ευκλείδειο χώρο (δηλαδή στο επίπεδο με μηδενική καμπυλότητα) το 5ο αίτημα αποδεικνύεται. Μάλιστα πιστεύω πως το έχω αποδείξει. Άλλωστε δεν υπάρχουν άλυτα προβλήματα αλλά πολύ δύσκολα στην απόδειξη προβλήματα.

Στον το 5ο αίτημα ισχύει. Όμως αυτό δεν σημαίνει ότι το 5ο αίτημα αποδεικνύεται από τα άλλα 4.
Αυτό επειδή το είναι ένα μοντέλο της ευκλείδειας γεωμετρίας. Όμως υπάρχουν άλλα μοντέλα της ευκλείδειας γεωμετρίας που το 5ο αίτημα δεν ισχύει. π.χ. η ευκλείδεια γεωμετρία στο εσωτερικό ενός κύκλου.
Άρα το 5ο αίτημα είναι ανεξάρτητο από τα άλλα τέσσερα.
Δηλαδή δεν αποδεικνύεται ούτε αυτό ούτε η άρνησή του από τα άλλα αξιώματα.

[sokrazara]

Θέλετε να σας στείλω με μορφή pdf την απόπειρα μου?

[sokrazara]

Η απόπειρα αφορά την απόδειξη του 5ου αιτήματος στο R^2 και έχει μια πρωτοποριακή ματιά του R^2. Εφόσον ισχύει στο R^2 θα πρέπει να συμβαδίζει με τις θεμελιώδεις ιδιότητες του R^2. Από εκεί έγκυται η απόδειξη

[stranger]

Όπως είπα και πριν στον είναι γνωστό ότι ισχύει.
Αυτό δεν σημαίνει όμως ότι το 5ο αίτημα αποδεικνύεται από τα άλλα τέσσερα.
Άλλο το , άλλο η γεωμετρία του ευκλείδη.
Στείλε αν θες αυτά που έχεις γράψει,μπορεί να έχουν ενδιαφέρον.

[sokrazara]

Αρχικά είμαι ένας μαθητής της 1ης λυκείου

[sokrazara]

Επίσης έγραψα μια εργασία 20 σελίδων περίπου που εργάζομαι για αυτήν την απόδειξη

[sokrazara]

Πιστευτώ πως είναι άρτια εργασία

[sokrazara]

Παρά το όριο της ηλικίας μου είναι ενδιαφέρουσα εργασία

[Mihalis_Lambrou]

Η αποπειρα αφορα την αποδειξη του 5ου αιτηματοσ στο R^2 και εχει μια πρωτοποριακη ματια του R^2. Εφοσον ισχυει στο R^2 θα πρεπει να συμβαδιζει με τισ θεμελιωδεισ ιδιοτητεσ του R^2. Απο εκει εγκυτε η αποδειξη

Καλώς ήλθες στο mathematica.

Ας ξεκαθαρίσουμε εξ αρχής ότι επειδή το πέμπτο αίτημα είναι ανεξάρτητο από τα υπόλοιπα, η απόδειξή σου έχει σίγουρα λάθος. ΣΙΓΟΥΡΑ. Αυτό δεν σημαίνει ότι σε αποθαρρύνουμε να ασχολείσαι με Μαθηματικά. Το αντίθετο, σε ενθαρρύνουμε και με χαρά θα διαβάσουμε την εργασία σου για να σου επισημάνουμε που είναι τα λάθη. Έτσι θα ωφεληθείς αφού όλοι μαθαίνουμε από τα λάθη μας.

Ομολογώ ότι εξ αρχής έχω σοβαρές επιφυλάξεις για το κείμενό σου γιατί αν το επίπεδό του είναι στο ίδιο επίπεδο επιτήδευσης με τα Ελληνικά που γράφεις, έχουμε πρόβλημα. Υπόψη οι λέξεις στα Ελληνικά τονίζονται, υπάρχει τελικό σίγμα και τα ρήματα της Μέσης φωνής έχουν άλλη ορθογραφία από αυτήν που γράφεις (υπόψη ότι υπάρχουν δωρεάν προγράμματα που κάνουν διόρθωση ορθογραφίας).

[sokrazara]

Αν αποδείξω ότι 2 παράλληλες ευθείες έχουν εντός εναλλάξ γωνίες ίσες τότε αυτό είναι ισοδύναμο του 5ου αιτήματος;

[Mihalis_Lambrou]

Αν αποδείξω ότι 2 παράλληλες ευθείες έχουν εντός εναλλάξ γωνίες ίσες τότε αυτό είναι ισοδύναμο του 5ου αιτήματος;

Ξεκινάς με την υπόθεση ότι υπάρχουν παράλληλες ευθείες, οπότε ήδη είναι προβληματική η απόδειξή σου.

Αλλά ας αφήσουμε τα πολλά λόγια. Επειδή απαντάς με ερώτηση και όχι επί της ουσίας, καλό είναι να κόψουμε την συζήτηση περί της απόδειξης και ας δούμε την ίδια την απόδειξη. Όλα τα άλλα είναι συζήτηση άνευ περιεχομένου.

Αν θέλεις να σου πούμε την γνώμη μας για την προσπάθειά σου, πρέπει να την δούμε. Το να ακούμε μόνο ότι υπάρχει απόδειξη του 5ου αιτήματος, είναι λόγια χωρίς αντίκρυσμα.

[Mihalis_Lambrou]

Sokrazara βλέπω ότι μπαίνεις όλη μέρα στο mathematica αλλά δεν φαίνεται να θέλεις να μας πεις την μέθοδό σου.

Συγκεκριμένα,

α) απόδειξη του 5ου αιτήματος και

β) (που εμένα προσωπικά με ενδιαφέρει περισσότερο) την πρωτοποριακή ματιά του , όπως αναφέρεις στο ποστ #5.

Πολύ θα ήθελα να έβλεπα το β).

Αν δεν ξέρεις πώς να αναρτήσεις την εργασία σου εδώ, θα μπορούσες να την αναρτούσες κάπου αλλού (π.χ. στο Google Drive) και να μας δώσεις εδώ το λινκ.

Αλλιώς στείλε την εργασία σου στους Γενικούς Συντονιστές ή στους Διαχειριστές του φόρουμ και ζήτα τους να σε διευκολύνουν με το τεχνικό μέρος της ανάρτησης.

[sokrazara]

Καλημέρα σας,
Σας επισυνάπτω το αρχείο μου, με την απόπειρα να αποδείξω το 5ο Ευκλείδειο Αίτημα. Φαντάζομαι κι εγώ, ότι πιθανότατα θα υπάρχουν κάποια λάθη, λόγω περιορισμένων γνώσεων και ηλικίας. Παρόλα αυτά, η διαδικασία αυτή με γοήτευσε και εξακολουθεί να με γοητεύει, λόγω της αγάπης μου για τα μαθηματικά.
Ελπίζω να αναδειχτεί έστω, ότι υπάρχει μαθηματική λογική σε αυτή μου την προσπάθεια.
Ευχαριστώ εκ των προτέρων για το ενδιαφέρον και το χρόνο σας,
Με εκτίμηση,
Ζαραβίνας Σωκράτης, μαθητής Α΄ Λυκείου.

[Mihalis_Lambrou]

Καλημέρα σας,
Σας επισυνάπτω το αρχείο μου, με την απόπειρα να αποδείξω το 5ο Ευκλείδειο Αίτημα. Φαντάζομαι κι εγώ, ότι πιθανότατα θα υπάρχουν κάποια λάθη, λόγω περιορισμένων γνώσεων και ηλικίας. Παρόλα αυτά, η διαδικασία αυτή με γοήτευσε και εξακολουθεί να με γοητεύει, λόγω της αγάπης μου για τα μαθηματικά.
Ελπίζω να αναδειχτεί έστω, ότι υπάρχει μαθηματική λογική σε αυτή μου την προσπάθεια.
Ευχαριστώ εκ των προτέρων για το ενδιαφέρον και το χρόνο σας,
Με εκτίμηση,
Ζαραβίνας Σωκράτης, μαθητής Α΄ Λυκείου.

Εύγε που ασχολείσαι με τα Μαθηματικά και καλό είναι να συνεχίσεις. Έχεις όμως ακόμα ΠΑΡΑ πολλά να μάθεις και είμαι βέβαιος ότι θα τα χαρείς.

Για την ώρα, δυστυχώς, αυτά που γράφεις είναι πάρα πολύ εσφαλμένα. Θα μου επιτρέψεις να είμαι απόλυτα ακριβής στα σχόλιά μου γιατί αυτό απαιτεί η επιστήμη. Πέρα από το γεγονός ότι σε ενθαρρύνω να συνεχίσεις τα εργάζεσαι στα Μαθηματικά, δεν πρέπει να συγχέουμε την χαρά της δημιουργίας με κριτική της όταν είναι εσφαλμένη. Επί της ουσίας:

Στις πρώτες λίγες σελίδες του κειμένου σου δεν υπάρχει σχεδόν τίποτα σωστό.

Θα αφήσω το γεγονός ότι μιλάς για τοπολογική μελέτη του επιπέδου, ενώ δεν έχεις ορίσει καμία τοπολογία. Η Τοπολογία είναι πολύ συγκεκριμένη έννοια στα Μαθηματικά (απαιτεί π.χ. καθορισμό ποιων συνόλων θα ονομάζουμε ανοικτά, και λοιπά, τα οποία πρέπει να πληρούν κάποιες ιδιότητες ως προς την τομή και ένωσή τους). Δεν πρέπει να συγχέουμε την λέξη τοπολογία με την καθημερινή της έννοια, που είναι πιο κοντά σε αυτήν που έχει στον νου του ένας Τοπογράφος ή ένας Γεωγράφος.

Όρισες επίπεδο ως ένα υπερσύνολο του . Προφανώς αυτό είναι λάθος και εννοείς υποσύνολο. Αλλά και αυτό είναι εσφαλμένο γιατί τότε είναι επίπεδο π.χ. ένα σύνολο που αποτελείται από 2022 σημεία. Φυσικά δεν είναι.

Αμέσως παρακάτω ορίζεις ως καμπύλες τα υποσύνολα του . Δεν στέκει. Π.χ. τα σημεία σε ένα τόξο κύκλου δεν ικανοποιούν αυτή την ιδιότητα.

Ο ορισμός του μήκους καμπύλης που γράφεις δεν λέει τίποτα. Απλά λέει ότι το μήκος καμπύλης είναι το μήκος της.

Παρακάτω μιλάς για το εσωτερικό καμπύλης και ότι είναι ανοικτό. Μα αφού δεν έχεις ορίσει ανοικτά σύνολα της Τοπολογίας, δεν στέκει.

Ένα βασικό σου βήμα στην απόδειξη είναι ότι παίρνεις μία αλυσίδα κύκλων και ισχυρίζεσαι ότι μετά από κάποια πεπερασμένα βήματα θα φτάσεις στο επίπεδο . Αυτό δεν ισχύει π.χ. στο μοντέλο του ευκλείδειου χώρου κατά Poincare. Άσε που χρησιμοποιείς κρυφά το Αξίωμα Aρχιμήδη-Ευδόξου. Αλλά αν χρησιμοποιήσεις το εν λόγω αξίωμα είναι γνωστό και απλό ότι έχουμε Ευκλείδειο επίπεδο, του οποίου η απόδειξη υπάρχει σε όλα τα βιβλία μη Ευκλείδειας Γεωμετρίας. Δηλαδή δεν έχεις κάτι νέο.

Σταματώ εδώ γιατί δεν έχει νόημα να γράφω με το πληκτρολόγιο καθώς θέλουν σιδέρωμα τόσο πολλά σημεία που θα έγραφα μεγαλύτερο όγκο σχολίων από το ίδιο το κείμενο που σχολιάζω.

Για να κλείνω: Εύγε στην προσπάθειά σου αλλά κοίτα πρώτα τι υπάρχει στην βιβλιογραφία. Όπως είπε ο Νεύτων, ο ίδιος έβλεπε πιο μακριά γιατί στεκόταν σε πλάτες γιγάντων. Μη κάνεις, λοιπόν, το σφάλμα να νομίζεις ότι βλέπεις μακριά ενώ δεν έχεις τις βασικές γνώσεις και την υποδομή, η οποία άλλωστε είναι χιλιοειπωμένη και γνωστή.

Καλό διάβασμα και καλή συνέχεια.

[stranger]

Καλημέρα σας,
Σας επισυνάπτω το αρχείο μου, με την απόπειρα να αποδείξω το 5ο Ευκλείδειο Αίτημα. Φαντάζομαι κι εγώ, ότι πιθανότατα θα υπάρχουν κάποια λάθη, λόγω περιορισμένων γνώσεων και ηλικίας. Παρόλα αυτά, η διαδικασία αυτή με γοήτευσε και εξακολουθεί να με γοητεύει, λόγω της αγάπης μου για τα μαθηματικά.
Ελπίζω να αναδειχτεί έστω, ότι υπάρχει μαθηματική λογική σε αυτή μου την προσπάθεια.
Ευχαριστώ εκ των προτέρων για το ενδιαφέρον και το χρόνο σας,
Με εκτίμηση,
Ζαραβίνας Σωκράτης, μαθητής Α΄ Λυκείου.

Εντάξει, το καλό είναι ότι ασχολείσαι με μαθηματικά πολύ ανώτερα από αυτά που μαθαίνεις στην τάξη που είσαι.
Αυτό πρέπει να το ενθαρύνουμε. Έχεις πολλές αναζητήσεις επιστημονικές και προσπαθείς να τα μάθεις όλα γρήγορα.
Όμως η γνώση κατακτιέται με πολλά και σταθερά βήματα, που χρειάζεται και ο νεανικός ενθουσιασμός σου.
Αν επιλέξεις να σπουδάσεις μαθηματικά και ενδιαφέρεσαι για τα μαθηματικά, τότε πρέπει να πηγαίνεις αργά και σταθερά. Αφού κάνουμε κτήμα μας το Α μετά πάμε στο Β και όταν κατακτήσουμε και το Β, πάμε στο Γ.
Μη βιάζεσαι τόσο πολύ γιατί θα τα μάθεις όλα αυτά με πολλά κενά και μετά θα έχεις πρόβλημα στην κατανόηση.
Άργα και σταθερά λοιπόν και βήμα βήμα.
Το ταξίδι για το 50 χιλιόμετρα, ξενικά με ένα βήμα.