Προσδιορισμός πλήθους αριθμών ενός διαστήματος τιμών με κριτήρια
Συντονιστής: spyros
Προσδιορισμός πλήθους αριθμών ενός διαστήματος τιμών με κριτήρια
Ψάχνω κάτι συγκεκριμένο επάνω σε σύνολα διαφόρων αριθμών.
Πιο αναλυτικά, πως προκύπτει ο προσδιορισμός του πλήθους των αριθμών ενός συνόλου τιμών στο οποίο υπάρχει συγκεκριμένο βήμα.
Να κάνω ένα παράδειγμα για να πω τι εννοώ με την λέξη βήμα.
Έστω το α που ανήκει σε ένα κλειστό διάστημα τιμών [2, 4] με α να είναι φυσικός αριθμός. Σε αυτή την περίπτωση το πλήθος των αριθμών του συνόλου είναι 3 (2, 3, 4). Αν όμως το α θεωρηθεί δεκαδικός ή πραγματικός αριθμός τότε μπορεί να λάβει και ενδιάμεσες τιμές.
Ας θεωρήσουμε τώρα πως το α στο διάστημα [2, 4] ανήκει στους πραγματικούς και προχωράει με βήμα 0.5. Αυτό σημαίνει οτι από το 2 μέχρι το 4 θα έχουμε 5 αριθμούς. Αν το βήμα μειωθεί το πλήθος των αριθμών θα αυξηθεί. Με δοκιμές βρήκα εμπειρικά πως το πλήθος των αριθμών για ένα διάστημα [α,β] με α και β φυσικοί αριθμοί υπολογίζεται με από ((β-α)/βήμα) + 1.
Τι συμβαίνει όμως αν δεν έχουμε μόνο φυσικούς αριθμούς, δηλαδή αν έχουμε αρνητικούς αριθμούς ή αν τα άκρα του διαστήματος δηλαδή τα α και β γίνουν δεκαδικοί αριθμοί, ρητοί και άρρητοι αριθμοί κτλ.
Ο τύπος υπολογισμού του μέγιστου αριθμών που μπορούν να υπάρχουν σε ένα σύνολο με βάση το βήμα είναι αυτός που έγραψα πριν για όλα τα σύνολα ή υπάρχουν και άλλοι τύποι ανάλογα το είδος των αριθμών και διάκριση περιπτώσεων.
Ελπίζω να καταλάβατε τι ήθελα να γράψω και αν μπορείτε να μου προτείνετε κάποια αναλυτικότερη βιβλιογραφία επί του θέματος στο διαδίκτυο.
Ευχαριστώ.
Πιο αναλυτικά, πως προκύπτει ο προσδιορισμός του πλήθους των αριθμών ενός συνόλου τιμών στο οποίο υπάρχει συγκεκριμένο βήμα.
Να κάνω ένα παράδειγμα για να πω τι εννοώ με την λέξη βήμα.
Έστω το α που ανήκει σε ένα κλειστό διάστημα τιμών [2, 4] με α να είναι φυσικός αριθμός. Σε αυτή την περίπτωση το πλήθος των αριθμών του συνόλου είναι 3 (2, 3, 4). Αν όμως το α θεωρηθεί δεκαδικός ή πραγματικός αριθμός τότε μπορεί να λάβει και ενδιάμεσες τιμές.
Ας θεωρήσουμε τώρα πως το α στο διάστημα [2, 4] ανήκει στους πραγματικούς και προχωράει με βήμα 0.5. Αυτό σημαίνει οτι από το 2 μέχρι το 4 θα έχουμε 5 αριθμούς. Αν το βήμα μειωθεί το πλήθος των αριθμών θα αυξηθεί. Με δοκιμές βρήκα εμπειρικά πως το πλήθος των αριθμών για ένα διάστημα [α,β] με α και β φυσικοί αριθμοί υπολογίζεται με από ((β-α)/βήμα) + 1.
Τι συμβαίνει όμως αν δεν έχουμε μόνο φυσικούς αριθμούς, δηλαδή αν έχουμε αρνητικούς αριθμούς ή αν τα άκρα του διαστήματος δηλαδή τα α και β γίνουν δεκαδικοί αριθμοί, ρητοί και άρρητοι αριθμοί κτλ.
Ο τύπος υπολογισμού του μέγιστου αριθμών που μπορούν να υπάρχουν σε ένα σύνολο με βάση το βήμα είναι αυτός που έγραψα πριν για όλα τα σύνολα ή υπάρχουν και άλλοι τύποι ανάλογα το είδος των αριθμών και διάκριση περιπτώσεων.
Ελπίζω να καταλάβατε τι ήθελα να γράψω και αν μπορείτε να μου προτείνετε κάποια αναλυτικότερη βιβλιογραφία επί του θέματος στο διαδίκτυο.
Ευχαριστώ.
Λέξεις Κλειδιά:
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15764
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Προσδιορισμός πλήθους αριθμών ενός διαστήματος τιμών με κριτήρια
Ή δεν έχω καταλάβει τι ρωτάς ή ρωτάς κάτι απλούστατο.mecheng έγραψε: ↑Δευ Απρ 26, 2021 5:42 amΨάχνω κάτι συγκεκριμένο επάνω σε σύνολα διαφόρων αριθμών.
Πιο αναλυτικά, πως προκύπτει ο προσδιορισμός του πλήθους των αριθμών ενός συνόλου τιμών στο οποίο υπάρχει συγκεκριμένο βήμα.
Να κάνω ένα παράδειγμα για να πω τι εννοώ με την λέξη βήμα.
Έστω το α που ανήκει σε ένα κλειστό διάστημα τιμών [2, 4] με α να είναι φυσικός αριθμός. Σε αυτή την περίπτωση το πλήθος των αριθμών του συνόλου είναι 3 (2, 3, 4). Αν όμως το α θεωρηθεί δεκαδικός ή πραγματικός αριθμός τότε μπορεί να λάβει και ενδιάμεσες τιμές.
Ας θεωρήσουμε τώρα πως το α στο διάστημα [2, 4] ανήκει στους πραγματικούς και προχωράει με βήμα 0.5. Αυτό σημαίνει οτι από το 2 μέχρι το 4 θα έχουμε 5 αριθμούς. Αν το βήμα μειωθεί το πλήθος των αριθμών θα αυξηθεί. Με δοκιμές βρήκα εμπειρικά πως το πλήθος των αριθμών για ένα διάστημα [α,β] με α και β φυσικοί αριθμοί υπολογίζεται με από ((β-α)/βήμα) + 1.
Τι συμβαίνει όμως αν δεν έχουμε μόνο φυσικούς αριθμούς, δηλαδή αν έχουμε αρνητικούς αριθμούς ή αν τα άκρα του διαστήματος δηλαδή τα α και β γίνουν δεκαδικοί αριθμοί, ρητοί και άρρητοι αριθμοί κτλ.
Ο τύπος υπολογισμού του μέγιστου αριθμών που μπορούν να υπάρχουν σε ένα σύνολο με βάση το βήμα είναι αυτός που έγραψα πριν για όλα τα σύνολα ή υπάρχουν και άλλοι τύποι ανάλογα το είδος των αριθμών και διάκριση περιπτώσεων.
Ελπίζω να καταλάβατε τι ήθελα να γράψω και αν μπορείτε να μου προτείνετε κάποια αναλυτικότερη βιβλιογραφία επί του θέματος στο διαδίκτυο.
Ευχαριστώ.
Αν λοιπόν κατάλαβα καλά, δίνεται ένα διάστημα
![[p,q] [p,q]](/forum/ext/geomar/texintegr/latexrender/pictures/aed02bcd6f03b8ff0507b69f093e795a.png) , ένας αριθμός
, ένας αριθμός ![a\in [p,q] a\in [p,q]](/forum/ext/geomar/texintegr/latexrender/pictures/ee29bbe7bb6c3f1d36a9f77b71a8f7b0.png) και ένα "βήμα"
και ένα "βήμα" 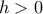 . Το ερώτημα είναι πόσοι αριθμοί υπάρχουν της μορφής
. Το ερώτημα είναι πόσοι αριθμοί υπάρχουν της μορφής  μέσα στο εν λόγω διάστημα. Σωστά; Αν ναι, η απάντηση είναι ότι υπάρχουν
μέσα στο εν λόγω διάστημα. Σωστά; Αν ναι, η απάντηση είναι ότι υπάρχουν  όροι όπου
όροι όπου  ο τέτοιος ώστε τελευταίος (ο πιο μεγάλος) όρος της ακολουθίας να είναι στο διάστημα. Δηλαδή θέλουμε τον μεγαλύτερο
ο τέτοιος ώστε τελευταίος (ο πιο μεγάλος) όρος της ακολουθίας να είναι στο διάστημα. Δηλαδή θέλουμε τον μεγαλύτερο  με
με  , ισοδύναμα
, ισοδύναμα  . Αν θέλουμε με σύμβολα (εδώ θα χρησιμοποιήσω το "ακέραιο μέρος") είναι εξ ορισμού
. Αν θέλουμε με σύμβολα (εδώ θα χρησιμοποιήσω το "ακέραιο μέρος") είναι εξ ορισμού ![\left [ \dfrac {q-a}{h} \right ] +1 \left [ \dfrac {q-a}{h} \right ] +1](/forum/ext/geomar/texintegr/latexrender/pictures/82f096b5db0a48af5f5acf808eac26d5.png)
Re: Προσδιορισμός πλήθους αριθμών ενός διαστήματος τιμών με κριτήρια
Αυτό ακριβώς που απάντησες έψαχνα.Mihalis_Lambrou έγραψε: ↑Δευ Απρ 26, 2021 7:51 amΉ δεν έχω καταλάβει τι ρωτάς ή ρωτάς κάτι απλούστατο.mecheng έγραψε: ↑Δευ Απρ 26, 2021 5:42 amΨάχνω κάτι συγκεκριμένο επάνω σε σύνολα διαφόρων αριθμών.
Πιο αναλυτικά, πως προκύπτει ο προσδιορισμός του πλήθους των αριθμών ενός συνόλου τιμών στο οποίο υπάρχει συγκεκριμένο βήμα.
Να κάνω ένα παράδειγμα για να πω τι εννοώ με την λέξη βήμα.
Έστω το α που ανήκει σε ένα κλειστό διάστημα τιμών [2, 4] με α να είναι φυσικός αριθμός. Σε αυτή την περίπτωση το πλήθος των αριθμών του συνόλου είναι 3 (2, 3, 4). Αν όμως το α θεωρηθεί δεκαδικός ή πραγματικός αριθμός τότε μπορεί να λάβει και ενδιάμεσες τιμές.
Ας θεωρήσουμε τώρα πως το α στο διάστημα [2, 4] ανήκει στους πραγματικούς και προχωράει με βήμα 0.5. Αυτό σημαίνει οτι από το 2 μέχρι το 4 θα έχουμε 5 αριθμούς. Αν το βήμα μειωθεί το πλήθος των αριθμών θα αυξηθεί. Με δοκιμές βρήκα εμπειρικά πως το πλήθος των αριθμών για ένα διάστημα [α,β] με α και β φυσικοί αριθμοί υπολογίζεται με από ((β-α)/βήμα) + 1.
Τι συμβαίνει όμως αν δεν έχουμε μόνο φυσικούς αριθμούς, δηλαδή αν έχουμε αρνητικούς αριθμούς ή αν τα άκρα του διαστήματος δηλαδή τα α και β γίνουν δεκαδικοί αριθμοί, ρητοί και άρρητοι αριθμοί κτλ.
Ο τύπος υπολογισμού του μέγιστου αριθμών που μπορούν να υπάρχουν σε ένα σύνολο με βάση το βήμα είναι αυτός που έγραψα πριν για όλα τα σύνολα ή υπάρχουν και άλλοι τύποι ανάλογα το είδος των αριθμών και διάκριση περιπτώσεων.
Ελπίζω να καταλάβατε τι ήθελα να γράψω και αν μπορείτε να μου προτείνετε κάποια αναλυτικότερη βιβλιογραφία επί του θέματος στο διαδίκτυο.
Ευχαριστώ.
Αν λοιπόν κατάλαβα καλά, δίνεται ένα διάστημα, ένας αριθμός
και ένα "βήμα"
. Το ερώτημα είναι πόσοι αριθμοί υπάρχουν της μορφής
μέσα στο εν λόγω διάστημα. Σωστά; Αν ναι, η απάντηση είναι ότι υπάρχουν
όροι όπου
ο τέτοιος ώστε τελευταίος (ο πιο μεγάλος) όρος της ακολουθίας να είναι στο διάστημα. Δηλαδή θέλουμε τον μεγαλύτερο
με
, ισοδύναμα
. Αν θέλουμε με σύμβολα (εδώ θα χρησιμοποιήσω το "ακέραιο μέρος") είναι εξ ορισμού
![\left [ \dfrac {q-a}{h} \right ] +1 \left [ \dfrac {q-a}{h} \right ] +1](/forum/ext/geomar/texintegr/latexrender/pictures/82f096b5db0a48af5f5acf808eac26d5.png)
Έδωσες τον ακριβή μαθηματικό ορισμό που με βοηθάει για ένα θέμα που ερευνώ.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 15 επισκέπτες
