Για να δούμε πόσες λύσεις θα βρεθούν.
Ισόπλευρο μέσα σε κανονικό εξάγωνο
Συντονιστής: Παύλος Μαραγκουδάκης
-
Παύλος Μαραγκουδάκης
- Επιμελητής
- Δημοσιεύσεις: 1513
- Εγγραφή: Παρ Ιαν 30, 2009 1:45 pm
- Τοποθεσία: Πειραιάς
- Επικοινωνία:
Ισόπλευρο μέσα σε κανονικό εξάγωνο
Να βρείτε το λόγο των εμβαδών του ισοπλεύρου προς το κανονικό εξάγωνο. Οι κορυφές του ισοπλεύρου είναι μέσα των πλευρών του εξαγώνου.
Για να δούμε πόσες λύσεις θα βρεθούν.
Για να δούμε πόσες λύσεις θα βρεθούν.
Στάλα τη στάλα το νερό το μάρμαρο τρυπά το,
εκείνο που μισεί κανείς γυρίζει κι αγαπά το.
εκείνο που μισεί κανείς γυρίζει κι αγαπά το.
Λέξεις Κλειδιά:
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13277
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: Ισόπλευρο μέσα σε κανονικό εξάγωνο
Καλησπέρα Παύλο! Τα μικρά έγχρωμα τριγωνάκια είναι ίσα και έστω ότι το καθένα έχει εμβαδόνΠαύλος Μαραγκουδάκης έγραψε: ↑Τετ Οκτ 18, 2017 3:53 pmΙσόπλευρο μέσα σε κανονικό εξάγωνο.png
Να βρείτε το λόγο των εμβαδών του ισοπλεύρου προς το κανονικό εξάγωνο. Οι κορυφές του ισοπλεύρου είναι μέσα των πλευρών του εξαγώνου.
Για να δούμε πόσες λύσεις θα βρεθούν.



- Μιχάλης Νάννος
- Επιμελητής
- Δημοσιεύσεις: 3537
- Εγγραφή: Δευ Ιαν 05, 2009 4:09 pm
- Τοποθεσία: Σαλαμίνα
- Επικοινωνία:
Re: Ισόπλευρο μέσα σε κανονικό εξάγωνο
Παύλος Μαραγκουδάκης έγραψε: ↑Τετ Οκτ 18, 2017 3:53 pm
Να βρείτε το λόγο των εμβαδών του ισοπλεύρου προς το κανονικό εξάγωνο. Οι κορυφές του ισοπλεύρου είναι μέσα των πλευρών του εξαγώνου.
Για να δούμε πόσες λύσεις θα βρεθούν.

«Δε θα αντικαταστήσει ο υπολογιστής τον καθηγητή...θα αντικατασταθεί ο καθηγητής που δεν ξέρει υπολογιστή...» - Arthur Clarke
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες

 και
και 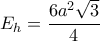 , συνεπώς :
, συνεπώς : 