Σελίδα 1 από 1
Διαιρετότητα με το 3
Δημοσιεύτηκε: Παρ Ιαν 27, 2023 7:45 pm
από ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
Θεωρούμε τους διψήφιους φυσικούς αριθμούς

. Γνωρίζουμε ότι οι

διαιρούμενοι με το

δίνουν
υπόλοιπο

αντιστοίχως.
Τοποθετούμε τα ψηφία των αριθμών αυτών σε μια σειρά με τυχαίο τρόπο και σχηματίζουμε τον εξαψήφιο αριθμό

Να εξηγήσετε γιατί το υπόλοιπο της διαίρεσης του

με το

θα είναι το

Re: Διαιρετότητα με το 3
Δημοσιεύτηκε: Παρ Ιαν 27, 2023 8:28 pm
από Τόλης
Γνωρίζουμε ότι ένας φυσικός αριθμός διαιρείται με το

, εάν το άθροισμα των ψηφίων του διαιρείται με το

.
Καθώς τα υπόλοιπα των αριθμών

διαιρώντας τα με το

, είναι

και

αντίστοιχα, γνωρίζουμε ότι
το άθροισμα των ψηφίων των αριθμών

διαιρώντας τα με το

έχουν υπόλοιπο

και

αντίστοιχα.
Οι αριθμοί

γράφονται ως εξής:

, όπου

και

ψηφία του αριθμού

και


, και


, και
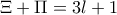
.
Ο εξαψήφιος αριθμός

που προκύπτει θα έχει ως ψηφία τα
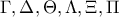
Το άθροισμα των ψηφίων του είναι

Αρά το υπόλοιπο της διαίρεσης του

με το

είναι

Re: Διαιρετότητα με το 3
Δημοσιεύτηκε: Παρ Ιαν 27, 2023 9:03 pm
από elenipappa
Έστω

Έχουμε

τρόπους τοποθέτησης των διψήφιων

για τον σχηματισμό του

.
Άρα διακρίνουμε τις εξής περιπτώσεις

.
Παίρνουμε τυχαία την περίπτωση


Όμως οι

είναι της μορφής

αντίστοιχα.
Άρα με αντικατάσταση στην


Επομένως, ο

αφήνει υπόλοιπο 1 όταν διαιρείται με το 3
 . Γνωρίζουμε ότι οι
. Γνωρίζουμε ότι οι  διαιρούμενοι με το
διαιρούμενοι με το  δίνουν
δίνουν  αντιστοίχως.
αντιστοίχως.
 με το
με το  θα είναι το
θα είναι το 
 . Γνωρίζουμε ότι οι
. Γνωρίζουμε ότι οι  διαιρούμενοι με το
διαιρούμενοι με το  δίνουν
δίνουν  αντιστοίχως.
αντιστοίχως.
 με το
με το  θα είναι το
θα είναι το 
 , εάν το άθροισμα των ψηφίων του διαιρείται με το
, εάν το άθροισμα των ψηφίων του διαιρείται με το  διαιρώντας τα με το
διαιρώντας τα με το  και
και  αντίστοιχα, γνωρίζουμε ότι
αντίστοιχα, γνωρίζουμε ότι  , όπου
, όπου  και
και  ψηφία του αριθμού
ψηφία του αριθμού  και
και 
 , και
, και 
 , και
, και 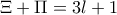 .
. που προκύπτει θα έχει ως ψηφία τα
που προκύπτει θα έχει ως ψηφία τα 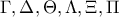


 τρόπους τοποθέτησης των διψήφιων
τρόπους τοποθέτησης των διψήφιων  για τον σχηματισμό του
για τον σχηματισμό του  .
. 

 αντίστοιχα.
αντίστοιχα. 