ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε:ΑΣΚΗΣΗ 73: Γράφουμε σε ένα χαρτίδιαδοχικούς περιττούς φυσικούς αριθμούς. Παρατηρήσαμε ότι αν διαγράψουμε
έναν συγκεκριμένο από αυτούς, τότε το άθροισμα των υπολοίπων πέντε αριθμών, έχει άθροισμα.
Να βρείτε ποιοι είναι οι έξι αριθμοί που είχαμε γράψει.
Διαγωνισμοί της ΕΜΕ-Α,Β Γυμνασίου
Συντονιστής: ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
Re: Διαγωνισμοί της ΕΜΕ-Α,Β Γυμνασίου
Bye :')
-
ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
- Επιμελητής
- Δημοσιεύσεις: 4770
- Εγγραφή: Τρί Αύγ 31, 2010 10:37 pm
- Τοποθεσία: Ιστιαία Ευβοίας
- Ορέστης Λιγνός
- Δημοσιεύσεις: 1835
- Εγγραφή: Κυρ Μάιος 08, 2016 7:19 pm
- Τοποθεσία: Χαλάνδρι Αττικής
- Επικοινωνία:
Re: Διαγωνισμοί της ΕΜΕ-Α,Β Γυμνασίου
Η εξίσωση γράφεταιΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε:ΑΣΚΗΣΗ 74: Αν, να λυθεί η εξίσωση:
 .
.Αν
 , με επαγωγή,
, με επαγωγή,  , οπότε με πρόσθεση αυτών,
, οπότε με πρόσθεση αυτών,  , άτοπο.
, άτοπο.Άρα,
 , και με δοκιμές
, και με δοκιμές  .
. Κερδίζουμε ό,τι τολμούμε!
-
ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
- Επιμελητής
- Δημοσιεύσεις: 4770
- Εγγραφή: Τρί Αύγ 31, 2010 10:37 pm
- Τοποθεσία: Ιστιαία Ευβοίας
Re: Διαγωνισμοί της ΕΜΕ-Α,Β Γυμνασίου
Γράφω αναλυτικά την λύση του JimNt:ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε:ΑΣΚΗΣΗ 74: Αν, να λυθεί η εξίσωση:
1η ΠΕΡΙΠΤΩΣΗ:
 . Τότε:
. Τότε:Ο αριθμός
 είναι περιττός, άρα περιττός θα είναι και ο
είναι περιττός, άρα περιττός θα είναι και ο 
Ο αριθμός 8 είναι άρτιος, άρα άρτιος θα είναι και ο

Συνεπώς ο αριθμός στο πρώτο μέλος είναι άρτιος.
Θα αποδείξουμε ότι ο αριθμός στο δεύτερο μέλος είναι περιττός
Πράγματι, αν
 άρτιος, τότε
άρτιος, τότε  περιττός και άρα το δεύτερο μέλος είναι περιττός
περιττός και άρα το δεύτερο μέλος είναι περιττόςΕνώ αν
 περιττός, τότε
περιττός, τότε  περιττός και άρα και πάλι το δεύτερο μέλος είναι περιττός
περιττός και άρα και πάλι το δεύτερο μέλος είναι περιττόςΆρα αν
 , τότε η εξίσωση είναι αδύνατη
, τότε η εξίσωση είναι αδύνατη2η ΠΕΡΙΠΤΩΣΗ:
 . Τότε εύκολα βλέπουμε ότι η εξίσωση επαληθεύεται.
. Τότε εύκολα βλέπουμε ότι η εξίσωση επαληθεύεται. Άρα η δοσμένη εξίσωση έχει μοναδική λύση την

Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες

 οι ζητούμενοι διαδοχικοί. Τότε αν πάρουμε τον ένα από αυτούς και αθροίσουμε τους υπόλοιπους θα προκύψει
οι ζητούμενοι διαδοχικοί. Τότε αν πάρουμε τον ένα από αυτούς και αθροίσουμε τους υπόλοιπους θα προκύψει 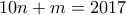

 . Πρέπει λοιπόν
. Πρέπει λοιπόν ![m ∈ [7,17,27] m ∈ [7,17,27]](/forum/ext/geomar/texintegr/latexrender/pictures/adfd9c80fffd5b321bb3e260159292de.png) (αφού η μέγιστη τιμή του
(αφού η μέγιστη τιμή του  είναι
είναι  . Βλέπουμε πως η ελάχιστη τιμή του
. Βλέπουμε πως η ελάχιστη τιμή του  . Επομένως,
. Επομένως,  . Εύκολα με δοκιμές προκύπτει ότι ο αριθμός που διαγράφουμε είναι ο
. Εύκολα με δοκιμές προκύπτει ότι ο αριθμός που διαγράφουμε είναι ο  . Επομένως είναι
. Επομένως είναι 
 . Εύκολα προκύπτουν οι ζητούμενοι...
. Εύκολα προκύπτουν οι ζητούμενοι...
 ,
,  , άτοπο...
, άτοπο...