Τομή πάνω στη διχοτόμο...

#1

Έστω ένα παραλληλόγραμμο $AB\Gamma\Delta$ . Πάνω στις πλευρές

και $B\Gamma$
λαμβάνουμε τα σημεία $K, \Lambda$ που είναι τέτοια ώστε να ισχύει $AK=\Gamma\Lambda$ .
Να αποδείξετε ότι η τομή των $A\Lambda, \Gamma K$ ανήκει πάνω στη διχοτόμο της γωνίας $A\widehat{\Delta}\Gamma$ .

STOPJOHN · #2

chris_gatos έγραψε: ↑
Σάβ Μαρ 06, 2021 8:35 pm
Έστω ένα παραλληλόγραμμο $AB\Gamma\Delta$ . Πάνω στις πλευρές και $B\Gamma$
λαμβάνουμε τα σημεία $K, \Lambda$ που είναι τέτοια ώστε να ισχύει $AK=\Gamma\Lambda$ .
Να αποδείξετε ότι η τομή των $A\Lambda, \Gamma K$ ανήκει πάνω στη διχοτόμο της γωνίας $A\widehat{\Delta}\Gamma$ .

Καλησπέρα Χρήστο

Εστω $AK=\Gamma \Lambda =t,B\Lambda =b-t,KB=a-t$

Στο τρίγωνο $KB\Gamma$ με τέμνουσα $AM\Lambda$ απο το Θ. Μενελάου είναι

$\dfrac{\Gamma M}{MK}\dfrac{AK}{AB}\dfrac{B\Lambda }{\Lambda \Gamma }=1\Rightarrow \dfrac{M\Gamma }{MK}=\dfrac{a}{b-t},(1), KN//\Delta \Gamma \Rightarrow \dfrac{M\Gamma }{MK}=\dfrac{a}{KN},(2) , (1),(2)\rightarrow KN=b-t$

Οπότε

$AN=t+b-t=b, \hat{N\Delta \Gamma }=\hat{AN\Delta },(3), A\Delta =AN\Rightarrow \hat{A\Delta ADN}=\hat{AN\Delta },(4), (3),(4)\Rightarrow \hat{A\Delta N}=\hat{N\Delta \Gamma }$

#3

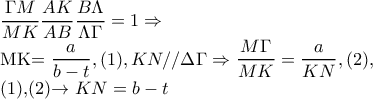
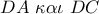Στις πλευρές $DA\,\,\kappa \alpha \iota \,\,DC$ θεωρώ σημεία $E\,\,\kappa \alpha \iota \,\,G$ για τα οποία :

$\boxed{DE = DG = LC = AK = m}$ .

: πάνω στη διχοτόμο_2.png (18.31 KiB) Προβλήθηκε 878 φορές

Αν

η διασταύρωση των $AL\,\,\kappa \alpha \iota \,\,CK$ και

η διασταύρωση των $EL\,\,\kappa \alpha \iota \,\,KG$ ,

προφανώς το τετράπλευρο ESGD

είναι ρόμβος και άρα η

διχοτόμος των γωνιών του στα $D\,\,\kappa \alpha \iota \,\,S$ .

Ας είναι ακόμα

το σημείο τομής των $AL\,\,\kappa \alpha \iota \,\,KG$ .

Αρκεί λοιπόν να δείξω ότι στο $\vartriangle STL$ η

είναι διχοτόμος . Αλλά ισχύουν ταυτόχρονα:

$\left\{ \begin{gathered} \frac{{SL}}{{ST}} = \frac{{EL}}{{EA}} = \frac{{AB}}{{BL}} \hfill \\ \frac{{FL}}{{FT}} = \frac{{LC}}{{KT}} = \frac{{AK}}{{KT}} = \frac{{AB}}{{BL}} \hfill \\ \end{gathered} \right. \Rightarrow \boxed{\frac{{SL}}{{ST}} = \frac{{FL}}{{FT}}}$ και αυτό που θέλω το έδειξα.

Μπορεί να λυθεί και με άλλους τρόπους.

Μιχάλης Τσουρακάκης · #4

chris_gatos έγραψε: ↑
Σάβ Μαρ 06, 2021 8:35 pm
Έστω ένα παραλληλόγραμμο $AB\Gamma\Delta$ . Πάνω στις πλευρές και $B\Gamma$
λαμβάνουμε τα σημεία $K, \Lambda$ που είναι τέτοια ώστε να ισχύει $AK=\Gamma\Lambda$ .
Να αποδείξετε ότι η τομή των $A\Lambda, \Gamma K$ ανήκει πάνω στη διχοτόμο της γωνίας $A\widehat{\Delta}\Gamma$ .

Η

τέμνει την

στο

και με $AH//KC \Rightarrow AK=HC=CL$

Από θ.κ.δέσμης $\dfrac{AZ}{ZH} = \dfrac{EM}{MC}= \dfrac{AM}{ML} \Rightarrow ZM//HL$ και οι πράσινες γωνίες είναι ίσες.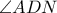

Επειδή και οι μπλε είναι ίσες ,η $\angle ADN$ είναι επίσης πράσινη,άρα

διχοτόμος

: τομή επί της διχοτόμου.png (17.96 KiB) Προβλήθηκε 874 φορές

#5

Έστω

τα αντίστοιχα ύψη, AK=CL=c

και αν

είναι το σημείο τομής των AL, CK

και

οι αποστάσεις του από τις AB, BC

αντίστοιχα, αρκεί να αποδείξουμε ότι το

ισαπέχει από τις AD, CD

αντίστοιχα.
Έτσι έχουμε :
$h_1-d_1=h_2-d_2\Leftrightarrow ch_1-cd_1=ch_2-cd_2\Leftrightarrow (ACK)-(MAK)=(ACL)-(CML) \Leftrightarrow ((MAC)=(MAC)$
και έχουμε τελειώσει.

Τομή πάνω στη διχοτόμο...

Τομή πάνω στη διχοτόμο...

Re: Τομή πάνω στη διχοτόμο...

Re: Τομή πάνω στη διχοτόμο...

Re: Τομή πάνω στη διχοτόμο...

Re: Τομή πάνω στη διχοτόμο...

Μέλη σε σύνδεση