Ναρκαλίευση και Γεωμετρία

[chris_gatos]

Ένας στρατιώτης (ναρκαλιευτής έμπειρος) πρέπει να ερευνήσει για την παρουσία ναρκών
σε ένα πεδίο που έχει σχήμα ισοπλεύρου τριγώνου.
Η ακτίνα δράσης του στρατιώτη ισούται με το μισό του ύψους του τριγώνου.
Βρίσκεται σε μια κορυφή του τριγώνου.
Ποιόν δρόμο θα τον συμβουλεύατε να ακολουθήσει ώστε να διατρέξει την ελάχιστη δυνατή απόσταση
αλλά και να εκπληρώσει την αποστολή του (να ελέγξει δηλαδή όλο αυτό το πεδίο);

Ελπίζω να σας ενδιαφέρει.
Χρόνια πολλά!

[Γιώργος Ρίζος]

Όντως ενδιαφέρον Χρήστο. Θα επιχειρήσω μια απάντηση:


Έστω η πλευρά του τριγώνου, τα μέσα των υψών του αντίστοιχα.

Το ύψος του τριγώνου είναι , άρα η ακτίνα του κύκλου είναι .


Όταν το σημείο (που αντιστοιχεί στη θέση του ναρκαλιευτή) είναι στη θέση , καλύπεται κυκλικός τομέας ακτίνας .

26-12-2020 Γεωμετρία a.png (49.28 KiB) Προβλήθηκε 1361 φορές

Το κινείται στη διαδρομή . Όταν βρεθεί στη θέση , ο κύκλος τέμνει τις και σε σημεία , , ώστε ώστε .
Έτσι, μένουν ακάλυπτα μόνον τα μεικτόγραμμα χωρία .

Κατόπιν κινείται στη διαδρομή LM και καλύπτει όλο το εσωτερικό του τριγώνου εκτός από τα μεικτόγραμμα χωρία , που έχουν ήδη καλυφθεί, εφόσον

26-12-2020 Γεωμετρία b.png (47.16 KiB) Προβλήθηκε 1361 φορές

Είναι και

Η διαδρομή είναι .

Επισυνάπτω ένα αρχείο Geogebra με κίνηση για τη διαδρομή του ναρκαλιευτή.

edit: Ξανακοιτώντας το, με την παρακίνηση του Χρήστου, βλέπω ότι ΔΕΝ είναι αναγκαίο να βρεθεί στα , αλλά σε κάποια από τα σημεία των τόξων . Άρα θα υπάρχει και κάποια καλύτερη προσέγγιση. Δεν τη βλέπω τώρα. Αν δεν υπάρξει ενδιαφέρον σε εύλογο χρόνο, θα ξαναπροσπαθήσω.

[Mihalis_Lambrou]

Και γιατί να μην σώσει τα σίγουρα την ζωή του με τίμημα να περπατήσει λίγο παραπάνω;

Αν μείνει στην ασφάλεια της περιμέτρου του τριγώνου μπορεί να πάει από το στο , στο , στο . Τι την θέλεις την Γεωμετρία
όταν κινδυνεύει η ζωή σου;

Narkes.png (49.17 KiB) Προβλήθηκε 1326 φορές

[Christos.N]

Εγώ δεν καταλαβαίνω αν ψάχνουμε κάλυψη ή την διαδρομή εκείνη που αν θεωρήσουμε κέντρα κύκλων θα έχουμε την βέλτιστη κάλυψη.

[Γιώργος Ρίζος]

Εγώ δεν καταλαβαίνω αν ψάχνουμε κάλυψη ή την διαδρομή εκείνη που αν θεωρήσουμε κέντρα κύκλων θα έχουμε την βέλτιστη κάλυψη.

Χρήστο, θέλει την ελάχιστη διαδρομή στο εσωτερικό του τριγώνου, ώστε ο κυκλικός δίσκος να καλύπτει (ανιχνεύει) πλήρως το εσωτερικό του τριγώνου.

edit: Ξανακοιτώντας το, με την παρακίνηση του Χρήστου Κυριαζή, βλέπω ότι ΔΕΝ είναι αναγκαίο να βρεθεί στα , αλλά σε κάποια από τα σημεία των τόξων . Άρα θα υπάρχει και κάποια καλύτερη προσέγγιση. Δεν τη βλέπω τώρα. Αν δεν υπάρξει ενδιαφέρον σε εύλογο χρόνο, θα ξαναπροσπαθήσω.

Με δοκιμές στο Geogebra, βελτίωσα τη διαδρομή: και κατόπιν στην ευθεία , ώσπου να συναντήσει το τόξο .
Mε τη βοήθεια ανισοτικών σχέσεων, πιστεύω πως μπορεί να αποδειχθεί ότι, είναι συντομότερη διαδρομή σε σχέση με άλλες από το προς κάποια σημεία των τόξων .
Επειδή ήδη έχω δεχτεί βοήθεια με σχετική υπόδειξη, το αφήνω για όποιον θα ήθελε να ασχοληθεί.

Το θεωρώ αρκετά ενδιαφέρον ως θέμα ερευνητικό, για να προκαλέσει συζητήσεις (σε μικρές, πολύ μικρές...) ομάδες μαθητών.
Για θέμα ΑΣΕΠ τι να πω... Θα έχει για μήνες λόξυγγα ο θεματοδότης από τις ευχές που θα ακούσει...

[Al.Koutsouridis]

Ένας στρατιώτης (ναρκαλιευτής έμπειρος) πρέπει να ερευνήσει για την παρουσία ναρκών
σε ένα πεδίο που έχει σχήμα ισοπλεύρου τριγώνου.
Η ακτίνα δράσης του στρατιώτη ισούται με το μισό του ύψους του τριγώνου.
Βρίσκεται σε μια κορυφή του τριγώνου.
Ποιόν δρόμο θα τον συμβουλεύατε να ακολουθήσει ώστε να διατρέξει την ελάχιστη δυνατή απόσταση
αλλά και να εκπληρώσει την αποστολή του (να ελέγξει δηλαδή όλο αυτό το πεδίο);

Χρόνια πολλά!

Οι σκέψεις μου ήταν οι εξείς αλλά δε είμαι σίγουρος και δεν είναι πλήρης λύση...

Έστω ότι ο ναρκαλιευτής βρίσκεται αρχικά στο σημείο του ισόπλευρου τριγώνου (πεδίου) . Επειδή εν τέλη θα πρέπει να ερευνήσει τα σημεία 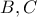θα πρέπει να βρεθεί σε ακτίνα (το ήμιση του ύψους του τριγώνου) από αυτά. Δηλαδή ο χώρος δράσης του αρκεί να είναι το εσωτερικό του τριγώνου εκτός των κυκλικών τομέων με κέντρα τα 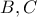και ακτίνα . Ο ναρκαλιευτής πρέπει να βρίσκεται τουλάχιστον στο σύνορο αυτών των κυκλικών τομέων για να καλύψει τα .

Φανταζόμαστε τώρα ότι ο ναρκαλιευτής τοποθέτησε κυκλικούς καθρέφτες (ως προς τα έξω ο καθρεπτισμός) στα σημεία 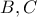με ακτίνα . Βρίσκεται στο σημείο και σημαδεύει το σημείο , που είναι τομή του κύκλου με το ύψος από το , με ένα λεϊζερ. Τότε παρατηρεί ότι η ακτίνα του λεϊζερ επιστρέφει σε αυτόν.

Το φώς όμως ακολουθεί την συνομότερη διαδρομή από το στο ύστερα στο (σημείο τομής του 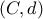με το τμήμα ) και πίσω. Αν ακολουθήσει αυτή την διαδρομή, που είναι διπλάσια από την ζητούμενη, παρατηρούμε ότι θα καλύψει όλο το τρίγωνο. Άρα η διαδρομή είναι η ζητούμενη (μία από αυτές).

narkalieuths.png (25.26 KiB) Προβλήθηκε 1210 φορές

[Μιχάλης Τσουρακάκης]

Ένας στρατιώτης (ναρκαλιευτής έμπειρος) πρέπει να ερευνήσει για την παρουσία ναρκών
σε ένα πεδίο που έχει σχήμα ισοπλεύρου τριγώνου.
Η ακτίνα δράσης του στρατιώτη ισούται με το μισό του ύψους του τριγώνου.
Βρίσκεται σε μια κορυφή του τριγώνου.
Ποιόν δρόμο θα τον συμβουλεύατε να ακολουθήσει ώστε να διατρέξει την ελάχιστη δυνατή απόσταση
αλλά και να εκπληρώσει την αποστολή του (να ελέγξει δηλαδή όλο αυτό το πεδίο);

Ελπίζω να σας ενδιαφέρει.
Χρόνια πολλά!

Θεωρούμε τους κυκλικούς τομείς του σχήματος ακτίνας και μέσα των

Το πρόβλημα ζητα, να ελέγξει όλη την επιφάνεια του ισόπλευρου τριγώνου, κανοντας συγχρόνως τη μικρότερη διαδρομή

Άν βρίσκεται στο έχει καλύψει τον τομέα .Για να ελέγξει την κορυφή κι όλο τον τομέα πρέπει

να κινηθεί στο τόξο και πρέπει να βρεθεί σε σημείο του ,τέτοιο ώστε κινούμενος

απ αυτό προς το τόξο για να ελέγξει τη κι όλο τον τομέα , να έχει κάνει τη μικρότερη διαδρομή

Αυτό ισοδυναμεί με την εύρεση της μικρότερης διαδρομής

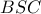
Θεωρώντας συμμετρικό του ως πρός την προφανώς τα είναι συνευθειακά

με . Ισχύει με το ελάχιστο να λαμβάνεται όταν

Άρα η ζητούμενη ελάχιστη διαδρομή ελέγχοντας όλη την επιφάνεια του τριγώνου είναι η

κι εύκολα βρίσκουμε ότι το μήκος αυτό είναι

ναρκαλιευτής.png (69.29 KiB) Προβλήθηκε 1180 φορές

[Christos.N]

Οι σκέψεις που έκανα (edit: με πειράματα)- αν κατάλαβα καλά ότι ψάχνουμε την διαδρομή των κέντρων του κύκλων που θα έχουν μέγιστη κάλυψη - συνοψίζονται στο επόμενο σχήμα.

Στιγμιότυπο από 2020-12-28 02-07-03.png (69.38 KiB) Προβλήθηκε 1138 φορές

Η εκκίνηση γίνεται πάνω σε πλευρά και στο σημείο που απέχει απο μια κορυφή μία ακτίνα, στην συνέχεια κινούμαστε προς το μέσο του ύψους που άγεται απο την έτερη κορυφή και τέλος κατευθυνόμαστε προς την απέναντι κορυφή.

edit2:

Ένας στρατιώτης (ναρκαλιευτής έμπειρος) πρέπει να ερευνήσει για την παρουσία ναρκών
σε ένα πεδίο που έχει σχήμα ισοπλεύρου τριγώνου.
Η ακτίνα δράσης του στρατιώτη ισούται με το μισό του ύψους του τριγώνου.
Βρίσκεται σε μια κορυφή του τριγώνου.
Ποιόν δρόμο θα τον συμβουλεύατε να ακολουθήσει ώστε να διατρέξει την ελάχιστη δυνατή απόσταση
αλλά και να εκπληρώσει την αποστολή του (να ελέγξει δηλαδή όλο αυτό το πεδίο);

δέκα φορές το διάβασα, μόλις είδα ότι η εκφώνηση γράφει σε κορύφη τριγώνου, το ξαναείδα γιατί βλέποντας τις λύσεις και των τριών όλοι συγκλίνατε. Πάω για ...σύντομα.

[chris_gatos]

Καλησπέρα και χρόνια πολλά!
Εύχομαι καλή χρονιά!
Να απολογηθώ γιατί σκόπευα να βάλω μια λύση όμως η χρονική στιγμή που έθεσα το πρόβλημα
ήταν αποτρεπτική έχοντας τρομερή κούραση από τη διαδικτυακή μου επαφή με τους μαθητές μου
αλλά και με τη διόρθωση πολλών (πάρα πολλών) ανορθόδοξων διαδικτυακών διαγωνισμάτων.
Τώρα μόλις άδειασα.
Ας είναι...
Πρωτοήρθα σε επαφή με την άσκηση από το διάβασμα των Γεωμετρικών θεμάτων του Μανόλη Μαραγκάκη.σελ(104)
Βρήκα άλλες δύο λύσεις, μια στο geometric problems on maxima and minima των T. Andreescu- O. Mushkarov-L. Stoyanov
και στο IMO Compendium των D.Djukic- V. Janković, I. Matić , N. Petrović.
Δεν είμαι και ο τελειότερος γεωμέτρης, μάλλον ερασιτέχνης θα έλεγα αλλά μου κίνησε το ενδιαφέρον. Για να είμαι ειλικρινής προσπάθησα
να το βάλω κάτω και να σκεφτώ τι ακριβώς ήθελε. Βάζοντας το και εδώ αλλά και σε άλλο φόρουμ είδα ότι οι προσεγγίσεις ποικίλλουν
και εκεί ακριβώς είναι το πρόβλημά μου.
Να πω πως η λύση που με ικανοποίησε και κατανόησα πλήρως (εγώ δεν τα κατάφερα μόνος) είναι από το τρίτο βιβλίο που αναφέρω (ήταν η επίσημη λύση του διαγωνισμού IMO ΤΟ 1973) και μοιάζει πολύ με τη λύση του Μιχάλη Τσουρακάκη.
Το ερώτημα μου είναι πόσο ασφαλές είναι το problem solving αλλά και πόσο μεγάλη σημασία παίζει μια σωστή εκφώνηση. Με τη συγκεκριμένη, το επαναλαμβάνω είχα θέμα, αλλά μπορεί η δική μου προσέγγιση ή το background που έχω να μη βοηθά!
Ευχαριστώ όλους όσους ασχολήθηκαν και "έσπασαν" το κεφάλι τους όπως κι εγώ για να δώσουν τα φώτα τους στο θέμα.
Ξανά καλή χρονιά και υγεία!

[chris_gatos]

Το θεωρώ αρκετά ενδιαφέρον ως θέμα ερευνητικό, για να προκαλέσει συζητήσεις (σε μικρές, πολύ μικρές...) ομάδες μαθητών.
Για θέμα ΑΣΕΠ τι να πω... Θα έχει για μήνες λόξυγγα ο θεματοδότης από τις ευχές που θα ακούσει...

Να πω επίσης ότι έχω πάρει την απόφαση να βάζω στη στήλη και θέματα που φυσικά δεν ενδείκνυνται για ΑΣΕΠ, όπως αυτό, αλλά
θα δώσουν πολλά αν ασχολούμαστε με αυτά (πάντα με προσωπικό γούστο και αναλαμβάνω όλη την ευθύνη επιλογής).
Γιώργο όντως θα είχε πονοκέφαλο για πολύ καιρό όποιος το τολμούσε!
Καλή συνέχεια!