 είναι σε αριθμητική πρόοδο
είναι σε αριθμητική πρόοδο και η μικρότερη γωνία του τριγώνου διαφέρει από τη μεγαλύτερη κατά
 .
.Να υπολογίσετε τις πλευρές του τριγώνου.
**Εννοούσα διαδοχικοί όροι αριθμητικής προόδου. Συγνώμη αν κάποιοι μπερδεύτηκαν.
Ευχαριστώ την Μαρία Σαμπάνη για την υπόδειξη.

 και τότε
και τότε 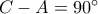 και
και  . Τότε λόγω της
. Τότε λόγω της  έχουμε
έχουμε 


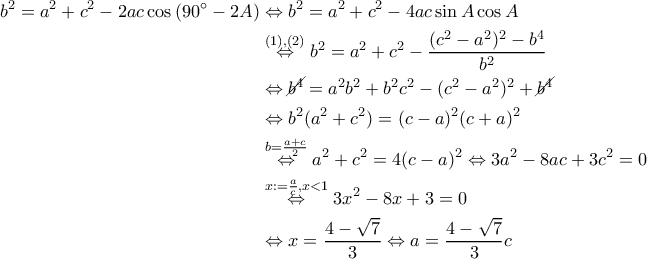
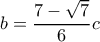
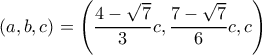
 και λόγω της προόδου
και λόγω της προόδου 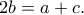



 είναι η διάμετρος του περιγεγραμμένου κύκλου και
είναι η διάμετρος του περιγεγραμμένου κύκλου και  η προβολή του
η προβολή του  στην
στην  τότε
τότε  οπότε
οπότε  είναι ισοσκελές τραπέζιο. Επίσης,
είναι ισοσκελές τραπέζιο. Επίσης, 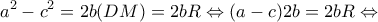
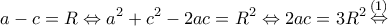

 η διαφορά της προόδου θα είναι
η διαφορά της προόδου θα είναι  άρα
άρα 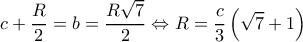


 και
και  η διχοτόμος της γωνίας
η διχοτόμος της γωνίας  , τότε
, τότε 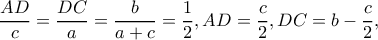 Εστω ότι
Εστω ότι  Τότε
Τότε 
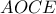 είναι εγράψιμο ,γιατί
είναι εγράψιμο ,γιατί 

 είναι ισοσκελές ,
είναι ισοσκελές ,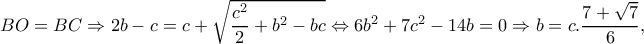



 και
και 
 η ακτίνα του περιγεγραμμένου κύκλου του.
η ακτίνα του περιγεγραμμένου κύκλου του.
 , οπότε, από (4) και (2) έχουμε
, οπότε, από (4) και (2) έχουμε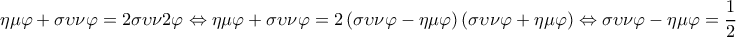 (5)
(5) , οπότε, λόγω της (5), είναι
, οπότε, λόγω της (5), είναι  (6).
(6). ,
, και
και  .
.
 , είναι
, είναι 