 είναι ορθογώνιο αν και μόνο αν:
είναι ορθογώνιο αν και μόνο αν: 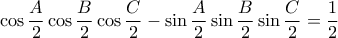
Συντονιστής: chris_gatos
Καλησπέρα Γιώργοgeorge visvikis έγραψε: ↑Τρί Δεκ 11, 2018 12:24 pmΝα δείξετε ότι το τρίγωνοείναι ορθογώνιο αν και μόνο αν:
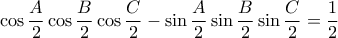
![cos\dfrac{A}{2}.cos\dfrac{B}{2}.cos\dfrac{C}{2}-sin\dfrac{A}{2}.sin\dfrac{B}{2}.sin\dfrac{C} 2}=\dfrac{1}{2}\
[cos(\dfrac{A}{2}+\dfrac{B}{2})+ cos(\dfrac{A}{2}-\dfrac{B}{2})]cos\dfrac{C} {2}
-[cos(\dfrac{A}{2}-\dfrac{B}{2})-cos(\dfrac{A}{2}+\dfrac{B}{2})]sin\dfrac{C}{2}=1\Leftrightarrow (sinA-
cosA)+(sin B-cosB)+(sin C-cosC)=1\Leftrightarrow sin(A-\dfrac{\pi }{4})+sin(B-\dfrac{\pi }{4})+sin(C-\dfrac{\pi
}{4})
=\dfrac{\sqrt{2}}{2}, cos\dfrac{A}{2}.cos\dfrac{B}{2}.cos\dfrac{C}{2}-sin\dfrac{A}{2}.sin\dfrac{B}{2}.sin\dfrac{C} 2}=\dfrac{1}{2}\
[cos(\dfrac{A}{2}+\dfrac{B}{2})+ cos(\dfrac{A}{2}-\dfrac{B}{2})]cos\dfrac{C} {2}
-[cos(\dfrac{A}{2}-\dfrac{B}{2})-cos(\dfrac{A}{2}+\dfrac{B}{2})]sin\dfrac{C}{2}=1\Leftrightarrow (sinA-
cosA)+(sin B-cosB)+(sin C-cosC)=1\Leftrightarrow sin(A-\dfrac{\pi }{4})+sin(B-\dfrac{\pi }{4})+sin(C-\dfrac{\pi
}{4})
=\dfrac{\sqrt{2}}{2},](/forum/ext/geomar/texintegr/latexrender/pictures/eb806de5decb61947f6f48f28e565b54.png)


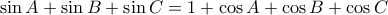



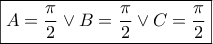
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες