 και η γραμμική συνάρτηση
και η γραμμική συνάρτηση 
για την οποία ισχύει
![\displaystyle \left| {f(x)} \right| \le 1,{\rm{ }}\forall {\rm{x}} \in \left[ {0,1} \right] \displaystyle \left| {f(x)} \right| \le 1,{\rm{ }}\forall {\rm{x}} \in \left[ {0,1} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/5f4ee1f19772efe13cfa35df191348bc.png) .
.Ποια είναι τότε η μέγιστη τιμή του γινομένου
 ;
;Συντονιστής: chris_gatos
 και η γραμμική συνάρτηση
και η γραμμική συνάρτηση 
![\displaystyle \left| {f(x)} \right| \le 1,{\rm{ }}\forall {\rm{x}} \in \left[ {0,1} \right] \displaystyle \left| {f(x)} \right| \le 1,{\rm{ }}\forall {\rm{x}} \in \left[ {0,1} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/5f4ee1f19772efe13cfa35df191348bc.png) .
. ;
;Hchris_gatos έγραψε: ↑Πέμ Δεκ 06, 2018 10:21 pmΈστωκαι η γραμμική συνάρτηση

για την οποία ισχύει.
Ποια είναι τότε η μέγιστη τιμή του γινομένου;
 δίνει
δίνει  . Άρα
. Άρα  .
.  της
της  που βέβαια ικανοποιεί την συνθήκη διότι
που βέβαια ικανοποιεί την συνθήκη διότι  , δίνουν
, δίνουν  . Με άλλα λόγια η μέγιστη τιμή του γινομένου
. Με άλλα λόγια η μέγιστη τιμή του γινομένου  είναι
είναι  .
.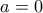 ή
ή  , τότε
, τότε  .
. ετερόσημοι τότε
ετερόσημοι τότε  .
. . Τότε η συνθήκη
. Τότε η συνθήκη ![\displaystyle \left| {f(x)} \right| \le 1,\forall {\rm{x}} \in \left[ {0,1} \right] \displaystyle \left| {f(x)} \right| \le 1,\forall {\rm{x}} \in \left[ {0,1} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/fd2a0b8f4f470aeff05a8f191f4cda50.png) της υποθέσεως γίνεται
της υποθέσεως γίνεται  (1).
(1). είναι
είναι  .
.![\displaystyle \forall x \in \left[ {0,\;1} \right] \displaystyle \forall x \in \left[ {0,\;1} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/78bb3d3ccbb82d7c41ed298fc4ea8104.png) είναι
είναι  .
.  . Όταν το άθροισμα
. Όταν το άθροισμα  ισούται με το μέγιστο δυνατό, που είναι
ισούται με το μέγιστο δυνατό, που είναι  , το γινόμενο
, το γινόμενο 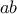 παίρνει τη μέγιστη τιμή του, όταν
παίρνει τη μέγιστη τιμή του, όταν  , οπότε το μέγιστο του γινομένου τους ισούται με
, οπότε το μέγιστο του γινομένου τους ισούται με  .
. . Τότε η συνθήκη
. Τότε η συνθήκη ![\displaystyle \left| {f(x)} \right| \le 1,\forall {\rm{x}} \in \left[ {0,1} \right] \displaystyle \left| {f(x)} \right| \le 1,\forall {\rm{x}} \in \left[ {0,1} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/fd2a0b8f4f470aeff05a8f191f4cda50.png) της υποθέσεως γίνεται
της υποθέσεως γίνεται  (2).
(2). είναι
είναι  .
.![\displaystyle \forall x \in \left[ {0,\;1} \right] \displaystyle \forall x \in \left[ {0,\;1} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/78bb3d3ccbb82d7c41ed298fc4ea8104.png) είναι
είναι  .
. . Όταν το άθροισμα των θετικών αριθμών
. Όταν το άθροισμα των θετικών αριθμών  ισούται με το μέγιστο δυνατό, που είναι
ισούται με το μέγιστο δυνατό, που είναι  , το γινόμενο
, το γινόμενο  παίρνει τη μέγιστη τιμή του, όταν
παίρνει τη μέγιστη τιμή του, όταν  , οπότε το μέγιστο του γινομένου τους ισούται με
, οπότε το μέγιστο του γινομένου τους ισούται με  .
. και
και  οπότε
οπότε 


 είναι
είναι  , όταν
, όταν ![x\in \left [ 0,1 \right ] x\in \left [ 0,1 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/6c33a6c363fd621c68b448a8bcad2f84.png) .
. αρκεί
αρκεί  .
. που ικανοποιούν τη συνθήκη
που ικανοποιούν τη συνθήκη 


 με την ισότητα για
με την ισότητα για 
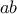 είναι
είναι  (αν δεν έκανα κάποιο άλμα...)
(αν δεν έκανα κάποιο άλμα...)Κάτι δεν μου πάει καλά με το παραπάνω βήμα. Πρώτα απ' όλα δεν είναι συντακτικά σωστό: Αν πούμε "επειδή" μετά πρέπει να πούμε "έπεται" και όχι "αρκεί".
 χάνουμε συναρτήσεις
χάνουμε συναρτήσεις  με
με  . Τέτοια είναι η
. Τέτοια είναι η  . Για να πεισθούμε ότι ικανοποιείται η
. Για να πεισθούμε ότι ικανοποιείται η  δεν έχουμε παρά να κοιτάξουμε το γράφημά της (απλό). Όμως εδώ
δεν έχουμε παρά να κοιτάξουμε το γράφημά της (απλό). Όμως εδώ  .
.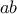 εκείνων των
εκείνων των  με
με  . Όμως υπάρχουν και άλλες
. Όμως υπάρχουν και άλλες  που ικανοποιούν τα δεδομένα της εκφώνησης, οπότε το μέγιστο
που ικανοποιούν τα δεδομένα της εκφώνησης, οπότε το μέγιστο 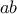 μπορεί να αυξηθεί.
μπορεί να αυξηθεί.Καλημέρα σε όλους. Έκανα μια προσπάθεια να παρέμβω στην λύση του Κώστα, αλλά δεν μπορώ να "σώσω την παρτίδα", όπως έλεγε ο αξέχαστος φίλος Λεωνίδας.Μπουμπουλής Κώστας έγραψε: ↑Κυρ Δεκ 09, 2018 1:00 amΑν μπορεί κάποιος να άρει το άλμα ας το κάνει , αν όχι ας αφαιρέσει παρακαλώ τη λύση ...
 και
και ![\displaystyle \vec v = \left( {x,1} \right),\;\;x \in \left[ {0,1} \right] \displaystyle \vec v = \left( {x,1} \right),\;\;x \in \left[ {0,1} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/bf2d97ebbb0971be6d4f4581ceaf8da5.png) οπότε
οπότε  .
. (1) , αφού η μέγιστη τιμή του
(1) , αφού η μέγιστη τιμή του  είναι
είναι  , όταν
, όταν ![\displaystyle x \in \left[ {0,1} \right] \displaystyle x \in \left[ {0,1} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/4987ba4cf4510bdf68a9f05777424a28.png) .
. ).
). γράφεται
γράφεται  (2), αφού
(2), αφού ![\displaystyle x \in \left[ {0,1} \right] \displaystyle x \in \left[ {0,1} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/4987ba4cf4510bdf68a9f05777424a28.png) .
. , για κάθε
, για κάθε  .
. .
.  , άρα η μέγιστη δυνατή τιμή του
, άρα η μέγιστη δυνατή τιμή του  είναι το
είναι το  , οπότε και το μέγιστο δυνατό γινόμενο
, οπότε και το μέγιστο δυνατό γινόμενο  είναι
είναι  .
. στη συνθήκη της υπόθεσης είναι η βέλτιστη.
στη συνθήκη της υπόθεσης είναι η βέλτιστη.Αρκεί να βρούμε το μέγιστο τουchris_gatos έγραψε: ↑Πέμ Δεκ 06, 2018 10:21 pmΈστωκαι η γραμμική συνάρτηση

για την οποία ισχύει.
Ποια είναι τότε η μέγιστη τιμή του γινομένου;

![x \in \left[ {0,1} \right],\;\left| {ax + b} \right| \leqslant 1 \Leftrightarrow {a^2}x + u \leqslant \left| a \right|. x \in \left[ {0,1} \right],\;\left| {ax + b} \right| \leqslant 1 \Leftrightarrow {a^2}x + u \leqslant \left| a \right|.](/forum/ext/geomar/texintegr/latexrender/pictures/3590113cacf597fbbd0be8220ba3a065.png) Αρκεί λοιπόν να βρούμε το
Αρκεί λοιπόν να βρούμε το  , όταν
, όταν  αφού
αφού ![x \in \left[ {0,1} \right] \Rightarrow u \leqslant {\left| a \right|^2}x + u \leqslant {\left| a \right|^2} + u, x \in \left[ {0,1} \right] \Rightarrow u \leqslant {\left| a \right|^2}x + u \leqslant {\left| a \right|^2} + u,](/forum/ext/geomar/texintegr/latexrender/pictures/c4e5bf14bbba096f840cc31c34db1e96.png) άρα αρκεί να βρούμε το
άρα αρκεί να βρούμε το  όταν
όταν  έτσι καταλήγουμε στην
έτσι καταλήγουμε στην  οπότε
οπότε  και αυτό γίνεται όταν
και αυτό γίνεται όταν  Η επαλήθευση είναι εύκολη.
Η επαλήθευση είναι εύκολη.
 βόσκουν σε ένα τετράγωνο
βόσκουν σε ένα τετράγωνο 
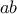
 η
η 

 παίρνουμε το ζητούμενο.
παίρνουμε το ζητούμενο. και
και  . Τότε
. Τότε
 και
και  . Μένει να κάνουμε τον απλό έλεγχο ότι η
. Μένει να κάνουμε τον απλό έλεγχο ότι η  ικανοποιεί τις συνθήκες.
ικανοποιεί τις συνθήκες.chris_gatos έγραψε: ↑Πέμ Δεκ 06, 2018 10:21 pmΈστωκαι η γραμμική συνάρτηση

για την οποία ισχύει.
Ποια είναι τότε η μέγιστη τιμή του γινομένου;

 μπορούμε χωρίς βλάβη της γενικότητας, να υποθέσουμε
μπορούμε χωρίς βλάβη της γενικότητας, να υποθέσουμε  αφού
αφού 

 ισχύει για κάθε
ισχύει για κάθε ![x \in \left[ {0,1} \right], x \in \left[ {0,1} \right],](/forum/ext/geomar/texintegr/latexrender/pictures/1bb28983b8252de535b82a664ca7b63d.png) θα έχουμε:
θα έχουμε: ![\left[ {0,1} \right] \subseteq \left[ { - \frac{{1 + \beta }}{\alpha },\;\frac{{1 - \beta }}{\alpha }} \right] \Rightarrow \frac{{1 - \beta }}{\alpha } \geqslant 1 \left[ {0,1} \right] \subseteq \left[ { - \frac{{1 + \beta }}{\alpha },\;\frac{{1 - \beta }}{\alpha }} \right] \Rightarrow \frac{{1 - \beta }}{\alpha } \geqslant 1](/forum/ext/geomar/texintegr/latexrender/pictures/e47dcc38385e5431b0d977126f260e16.png)

 με το ισον για
με το ισον για  Προφανώς τότε
Προφανώς τότε 
 έχουμε
έχουμε  Άρα
Άρα 

 κλπ.(!!)
κλπ.(!!) ,
, 

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης