Ένα ωραίο θεμα!
Συντονιστής: Τηλέγραφος Κώστας
-
APOSTOLAKIS
- Δημοσιεύσεις: 142
- Εγγραφή: Δευ Δεκ 22, 2008 6:09 pm
Ένα ωραίο θεμα!
Δίνεται τρίγωνο ΟΑΒ και G το βαρύκεντρο του. Μια τυχαία ευθεία (ε) διέρχεται από το G και τέμνει τις ΟΑ, ΟΒ στα σημεία Ρ και Q αντίστοιχα έτσι ώστε διανυσμαΟΡ=h.διανυσμαΟΑ και διανυσμαΟQ=κ.διανυσμαΟΒ. Αν (ΟΑΒ)=S και (ΟPQ)=T, να αποδείξετε ότι:
(α). (1/h)+(1/κ)=3
(β). 4S/9 μικρότερο ή ίσο του Τ μικρότερο ή ίσο του S/2
(α). (1/h)+(1/κ)=3
(β). 4S/9 μικρότερο ή ίσο του Τ μικρότερο ή ίσο του S/2
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15763
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Ένα ωραίο θεμα!
Εργαζόμαστε με Αναλυτική Γεωμετρία. Το ευκολότερο είναι με πλαγιογώνιους άξονες, τους ΟΑ, ΟΒ αλλά επειδή είναι εκτός ύλης, θα το κάνω με ορθογώνιους.
Λοιπόν, με αρχή των αξόνων το Ο, τα Α, Β είναι Α(α,0), Β(β,γ) οπότε είναι P(hα,0),
Q(kβ,kγ) και G( (α+β)/3, γ/3). Το γεγονός ότι τα P,G, Q είναι συνευθειακά (άρα ηκλίση της PG ισούται με την κλίση της PQ) μεταφράζεται, μετά τις πράξεις, σε
3hk-k-h = 0, που ισοδυναμεί με την ζητούμενη.
Για το (β) θα υποθέσω ότi η PQ τέμνει τις πλευρές του τριγώνου εσωτερικά (αλλιώς η άσκηση δεν είναι σωστή), οπότε 0 < = k < = 1, 0 < = h < = 1.
Επειδή τα S, T έχουν κοινή την γωνία Ο είναι T/S = OA.OB/OP.OQ = 1/(hk). Ζητάμε λοιπόν τις ακραίες τιμές του 1/(hk) = (3h-1)/h^2, υπό τις συνθήκες
0 < = k < = 1, 0 < = h < = 1, 1/h = 3 – 1/k. Οι τρεις τελευταίες δίνουν ½ < = h < = 1.
Σε αυτό το διάστημα βρίσκουμε, με παραγώγιση, ακρότατα στα h = 2/3 και h = 1, που με τη σειρά τους δίνουν τις τιμές στο (β). Αντιστοιχούν σε διατέμνουσα που είτε διέρχεται από το Α (δηλαδή είναι διάμεσος) είτε είναι παράλληλη της βάσης ΑΒ.
Φιλικά,
Μιχάλης Λάμπρου.
Λοιπόν, με αρχή των αξόνων το Ο, τα Α, Β είναι Α(α,0), Β(β,γ) οπότε είναι P(hα,0),
Q(kβ,kγ) και G( (α+β)/3, γ/3). Το γεγονός ότι τα P,G, Q είναι συνευθειακά (άρα ηκλίση της PG ισούται με την κλίση της PQ) μεταφράζεται, μετά τις πράξεις, σε
3hk-k-h = 0, που ισοδυναμεί με την ζητούμενη.
Για το (β) θα υποθέσω ότi η PQ τέμνει τις πλευρές του τριγώνου εσωτερικά (αλλιώς η άσκηση δεν είναι σωστή), οπότε 0 < = k < = 1, 0 < = h < = 1.
Επειδή τα S, T έχουν κοινή την γωνία Ο είναι T/S = OA.OB/OP.OQ = 1/(hk). Ζητάμε λοιπόν τις ακραίες τιμές του 1/(hk) = (3h-1)/h^2, υπό τις συνθήκες
0 < = k < = 1, 0 < = h < = 1, 1/h = 3 – 1/k. Οι τρεις τελευταίες δίνουν ½ < = h < = 1.
Σε αυτό το διάστημα βρίσκουμε, με παραγώγιση, ακρότατα στα h = 2/3 και h = 1, που με τη σειρά τους δίνουν τις τιμές στο (β). Αντιστοιχούν σε διατέμνουσα που είτε διέρχεται από το Α (δηλαδή είναι διάμεσος) είτε είναι παράλληλη της βάσης ΑΒ.
Φιλικά,
Μιχάλης Λάμπρου.
- nsmavrogiannis
- Επιμελητής
- Δημοσιεύσεις: 4455
- Εγγραφή: Σάβ Δεκ 20, 2008 7:13 pm
- Τοποθεσία: Αθήνα
- Επικοινωνία:
Re: Ένα ωραίο θεμα!
Aν και τα είπε όλα ο Μιχάλης ανεβάζω και αυτήν αφ΄' ενός γιατί είναι μέσα στην ύλη της Β' Τάξης και αφ' ετέρου για να μην πάει χαμένος ο κόπος μου με τόσα βελάκια που έγραψα:
Ονομάζουμε ,
,  . Aς υποθέσουμε ότι η ΟG τέμνει την ΑΒ στο Γ και ότι
. Aς υποθέσουμε ότι η ΟG τέμνει την ΑΒ στο Γ και ότι  . Φυσικά
. Φυσικά  όπου
όπου 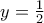 . Είναι ακόμη
. Είναι ακόμη  με
με  . Είναι
. Είναι  και
και  'Αρα
'Αρα 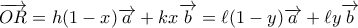 από την οποία βρίκουμε ότι
από την οποία βρίκουμε ότι  ,
,  και από αυτές εύκολα προκύπτει
και από αυτές εύκολα προκύπτει 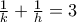 . Παίρνοντας τώρα τον λόγο των εμβαδών των δύο τριγώνων που είναι ίσος με το πηλίκο των γινομένων των πλευρών που άγονται από την κοινή κορυφή Ο βρίσκουμε ότι
. Παίρνοντας τώρα τον λόγο των εμβαδών των δύο τριγώνων που είναι ίσος με το πηλίκο των γινομένων των πλευρών που άγονται από την κοινή κορυφή Ο βρίσκουμε ότι  . Οπότε αρκεί
. Οπότε αρκεί  . Αφού
. Αφού 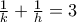 οι
οι είναι ρίζες του τριωνύμου
είναι ρίζες του τριωνύμου 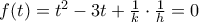 που για να έχει μη αρνητική διακρίνουσα πρέπει
που για να έχει μη αρνητική διακρίνουσα πρέπει  . Επίσης για να είναι τα P, Q εσωτερικά σημεία των αντιστοίχων πλευρών πρέπει να είναι
. Επίσης για να είναι τα P, Q εσωτερικά σημεία των αντιστοίχων πλευρών πρέπει να είναι  άρα
άρα  και επομένως πρέπει το
και επομένως πρέπει το 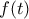 να έχει τις ρίζες του στο
να έχει τις ρίζες του στο ![(0,2] (0,2]](/forum/ext/geomar/texintegr/latexrender/pictures/eb1351ddf84d6ca6e06bbb319592766d.png) . Άρα το 2 ή θα είναι ρίζα είτε θα βρίσκεται εκτός των ριζών οπότε πρέπει
. Άρα το 2 ή θα είναι ρίζα είτε θα βρίσκεται εκτός των ριζών οπότε πρέπει  από την οποία προκύπτει ότι
από την οποία προκύπτει ότι 
Μαυρογιάννης
Ονομάζουμε
 ,
,  . Aς υποθέσουμε ότι η ΟG τέμνει την ΑΒ στο Γ και ότι
. Aς υποθέσουμε ότι η ΟG τέμνει την ΑΒ στο Γ και ότι  . Φυσικά
. Φυσικά  όπου
όπου 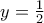 . Είναι ακόμη
. Είναι ακόμη  με
με  . Είναι
. Είναι  και
και  'Αρα
'Αρα 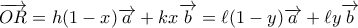 από την οποία βρίκουμε ότι
από την οποία βρίκουμε ότι  ,
,  και από αυτές εύκολα προκύπτει
και από αυτές εύκολα προκύπτει 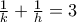 . Παίρνοντας τώρα τον λόγο των εμβαδών των δύο τριγώνων που είναι ίσος με το πηλίκο των γινομένων των πλευρών που άγονται από την κοινή κορυφή Ο βρίσκουμε ότι
. Παίρνοντας τώρα τον λόγο των εμβαδών των δύο τριγώνων που είναι ίσος με το πηλίκο των γινομένων των πλευρών που άγονται από την κοινή κορυφή Ο βρίσκουμε ότι  . Οπότε αρκεί
. Οπότε αρκεί  . Αφού
. Αφού 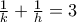 οι
οι είναι ρίζες του τριωνύμου
είναι ρίζες του τριωνύμου 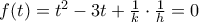 που για να έχει μη αρνητική διακρίνουσα πρέπει
που για να έχει μη αρνητική διακρίνουσα πρέπει  . Επίσης για να είναι τα P, Q εσωτερικά σημεία των αντιστοίχων πλευρών πρέπει να είναι
. Επίσης για να είναι τα P, Q εσωτερικά σημεία των αντιστοίχων πλευρών πρέπει να είναι  άρα
άρα  και επομένως πρέπει το
και επομένως πρέπει το 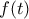 να έχει τις ρίζες του στο
να έχει τις ρίζες του στο ![(0,2] (0,2]](/forum/ext/geomar/texintegr/latexrender/pictures/eb1351ddf84d6ca6e06bbb319592766d.png) . Άρα το 2 ή θα είναι ρίζα είτε θα βρίσκεται εκτός των ριζών οπότε πρέπει
. Άρα το 2 ή θα είναι ρίζα είτε θα βρίσκεται εκτός των ριζών οπότε πρέπει  από την οποία προκύπτει ότι
από την οποία προκύπτει ότι 
Μαυρογιάννης
Αν κανείς δεν ελπίζει, δεν θα βρεί το ανέλπιστο, οι δρόμοι για το ανεξερεύνητο θα είναι κλειστοί.
Ηράκλειτος
Ηράκλειτος
Re: Ένα ωραίο θεμα!
Καλησπέρα σε όλους
Βάζω μια απόδειξη κλασικής γεωμετρίας την οποία θα ανεβάσω σε pdf όταν τελειώσω την μορφοποίησή της στο word
Πάνος
---- >>>Στη γραμμή Τ=(OPG)+(OQG) αμέσως μετά χρειάζεται ένα =
Βάζω μια απόδειξη κλασικής γεωμετρίας την οποία θα ανεβάσω σε pdf όταν τελειώσω την μορφοποίησή της στο word
Πάνος
---- >>>Στη γραμμή Τ=(OPG)+(OQG) αμέσως μετά χρειάζεται ένα =
- Συνημμένα
-
- geo1.png (27 KiB) Προβλήθηκε 3380 φορές
-
- geo2.png (38.89 KiB) Προβλήθηκε 3377 φορές
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15763
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Ένα ωραίο θεμα!
Η πολύ ωραία λύση του Πάνου μου έδωσε μία ιδέα για παρόμοια αλλά ίσως λίγο εποπτικότερη λύση του 2ου μέρους. Χάριν πληρότητας γράφω ολόκληρη την λύση (δηλαδή και του 1ου μέρους, η οποία είναι επανάληψη αυτής του Πάνου αλλά με δικά μου λόγια).
α) λύση ου Πάνου (math_finder)
Επειδή τα OPQ, ΟΑΒ έχουν κοινή την γωνία Ο είναι

Το ίδιο πηλίκο το υπολογίζουμε και αλλιώς:
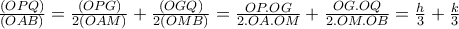
άρα hk=(h+k)/3 που ισοδυναμεί με το ζητούμενο.
β) Στο Σχήμα 1 η είναι παράλληλη στην βάση. Θα δείξουμε ότι το
είναι παράλληλη στην βάση. Θα δείξουμε ότι το  είναι το τρίγωνο ελάχιστου εμβαδού.
είναι το τρίγωνο ελάχιστου εμβαδού.
Πράγματι, αν φέρουμε παράλληλη στην ΟΒ τότε τα τρίγωνα
παράλληλη στην ΟΒ τότε τα τρίγωνα  ,
,  είναι ίσα (εδώ χρησιμοποιείται η ιδιότητα
είναι ίσα (εδώ χρησιμοποιείται η ιδιότητα  της διαμέσου). Εύκολα τώρα βλέπουμε ότι
της διαμέσου). Εύκολα τώρα βλέπουμε ότι  .
.
Στο Σχήμα 2 είναι (το G έχει ληφθεί κάτω από την παράλληλη στη βάση που διέρχεται από το G).
(το G έχει ληφθεί κάτω από την παράλληλη στη βάση που διέρχεται από το G).
Έτσι (GQΔ) (GPΓ) οπότε εύκολα βλέπουμε ότι (OPQ)
(GPΓ) οπότε εύκολα βλέπουμε ότι (OPQ) (OAΔ), δηλαδή το ΟΑΔ είναι το μέγιστο τρίγωνο.
(OAΔ), δηλαδή το ΟΑΔ είναι το μέγιστο τρίγωνο.
Δεδομένου ότι και (ΟΑΔ) = (ΟΑΒ)/2, έπονται οι ζητούμενες ανισώσεις.
και (ΟΑΔ) = (ΟΑΒ)/2, έπονται οι ζητούμενες ανισώσεις.
Φιλικά και με ευχαριστίες στον Πάνο για την ωραία του λύση.
Μιχάλης Λάμπρου
α) λύση ου Πάνου (math_finder)
Επειδή τα OPQ, ΟΑΒ έχουν κοινή την γωνία Ο είναι

Το ίδιο πηλίκο το υπολογίζουμε και αλλιώς:
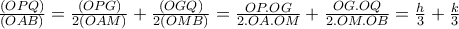
άρα hk=(h+k)/3 που ισοδυναμεί με το ζητούμενο.
β) Στο Σχήμα 1 η
 είναι παράλληλη στην βάση. Θα δείξουμε ότι το
είναι παράλληλη στην βάση. Θα δείξουμε ότι το  είναι το τρίγωνο ελάχιστου εμβαδού.
είναι το τρίγωνο ελάχιστου εμβαδού. Πράγματι, αν φέρουμε
 παράλληλη στην ΟΒ τότε τα τρίγωνα
παράλληλη στην ΟΒ τότε τα τρίγωνα  ,
,  είναι ίσα (εδώ χρησιμοποιείται η ιδιότητα
είναι ίσα (εδώ χρησιμοποιείται η ιδιότητα  της διαμέσου). Εύκολα τώρα βλέπουμε ότι
της διαμέσου). Εύκολα τώρα βλέπουμε ότι  .
.Στο Σχήμα 2 είναι
 (το G έχει ληφθεί κάτω από την παράλληλη στη βάση που διέρχεται από το G).
(το G έχει ληφθεί κάτω από την παράλληλη στη βάση που διέρχεται από το G). Έτσι (GQΔ)
 (GPΓ) οπότε εύκολα βλέπουμε ότι (OPQ)
(GPΓ) οπότε εύκολα βλέπουμε ότι (OPQ) (OAΔ), δηλαδή το ΟΑΔ είναι το μέγιστο τρίγωνο.
(OAΔ), δηλαδή το ΟΑΔ είναι το μέγιστο τρίγωνο. Δεδομένου ότι
 και (ΟΑΔ) = (ΟΑΒ)/2, έπονται οι ζητούμενες ανισώσεις.
και (ΟΑΔ) = (ΟΑΒ)/2, έπονται οι ζητούμενες ανισώσεις. Φιλικά και με ευχαριστίες στον Πάνο για την ωραία του λύση.
Μιχάλης Λάμπρου
- Συνημμένα
-
- και ελάχιστο τρίγωνο.JPG (18.4 KiB) Προβλήθηκε 3269 φορές
Re: Ένα ωραίο θεμα!
Άλλος τρόπος για την διπλή ανισότητα:
Είναι όπου
όπου 
Όμως είναι:

Επίσης είναι:

Επειδή![h,k\in[0,1] h,k\in[0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/545443a2ebe4fa6a484a4cb269a9a57c.png) και
και  παίρνουμε
παίρνουμε ![\displaystyle h,k\in\left[\frac{1}{2},1\right] \displaystyle h,k\in\left[\frac{1}{2},1\right]](/forum/ext/geomar/texintegr/latexrender/pictures/8c52323846b8e28b7a11311603fae4be.png) Επομένως είναι:
Επομένως είναι:

Αντικαθιστώντας στη (2) παίρνουμε που ισχύει.
που ισχύει.
Είναι
 όπου
όπου 
Όμως είναι:

Επίσης είναι:

Επειδή
![h,k\in[0,1] h,k\in[0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/545443a2ebe4fa6a484a4cb269a9a57c.png) και
και  παίρνουμε
παίρνουμε ![\displaystyle h,k\in\left[\frac{1}{2},1\right] \displaystyle h,k\in\left[\frac{1}{2},1\right]](/forum/ext/geomar/texintegr/latexrender/pictures/8c52323846b8e28b7a11311603fae4be.png) Επομένως είναι:
Επομένως είναι:
Αντικαθιστώντας στη (2) παίρνουμε
 που ισχύει.
που ισχύει.2ος νόμος του Μέρφυ: Τίποτα δεν είναι τόσο εύκολο, από όσο φαίνεται οτι είναι.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης
