Αναλυτική γεωμετρία με γεωμετρία

[fmak65]

Μια άσκηση του γιού μου για τους μαθητές του στο σχολείο.
Δίνονται τα σημεία Α,Β,Γ με Α(1,2), Β(7,4), Γ(3,8).
α) Να υπολογιστεί η εξίσωση του περιγεγραμμένου κύκλου του ΑΒΓ.
β) Να υπολογιστεί η περίμετρος και το εμβαδόν του ΑΒΓ.
γ) Να υπολογιστεί η ακτίνα του εγγεγραμμένου κύκλου του ΑΒΓ.
δ) Να υπολογιστεί η εξίσωση του εγγεγραμμένου κύκλου του ΑΒΓ.

[george visvikis]

Μια άσκηση του γιού μου για τους μαθητές του στο σχολείο.
Δίνονται τα σημεία Α,Β,Γ με Α(1,2), Β(7,4), Γ(3,8).
α) Να υπολογιστεί η εξίσωση του περιγεγραμμένου κύκλου του ΑΒΓ.
β) Να υπολογιστεί η περίμετρος και το εμβαδόν του ΑΒΓ.
γ) Να υπολογιστεί η ακτίνα του εγγεγραμμένου κύκλου του ΑΒΓ.
δ) Να υπολογιστεί η εξίσωση του εγγεγραμμένου κύκλου του ΑΒΓ.

α) Οι μεσοκάθετοι των έχουν αντίστοιχες εξισώσεις

Άρα και Επομένως η εξίσωση του περιγεγραμμένου κύκλου είναι:

Αναλυτική με Γεωμετρία.png (19.74 KiB) Προβλήθηκε 351 φορές

β) Εύκολα βρίσκω οπότε η περίμετρος είναι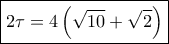

Όσο για το εμβαδόν, επιλέγω τον τύπο,

γ)

δ) Χρειαζόμαστε τις συντεταγμένες του έγκεντρου που βρίσκεται στην ευθεία και είναι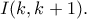

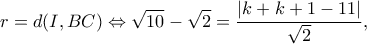απ' όπου παίρνω τη δεκτή ρίζα

Έτσι έχουμε την εξίσωση του εγγεγραμμένου κύκλου,