 , τέμνει τις πλευρές
, τέμνει τις πλευρές στα
στα  . Υποδείξτε στην πολεοδομία πως να φέρει αυτή την ευθεία , ώστε
. Υποδείξτε στην πολεοδομία πως να φέρει αυτή την ευθεία , ώστε το οικόπεδο που θα παραμείνει λευκό , να είναι όσο το δυνατόν μεγαλύτερο σε εμβαδόν .
Συντονιστής: Τηλέγραφος Κώστας
 , τέμνει τις πλευρές
, τέμνει τις πλευρές στα
στα  . Υποδείξτε στην πολεοδομία πως να φέρει αυτή την ευθεία , ώστε
. Υποδείξτε στην πολεοδομία πως να φέρει αυτή την ευθεία , ώστε Ισοδύναμα θέλουμε το ελάχιστο γαλάζιο τρίγωνο. Έστω λοιπόν
 (τα τελευταία βγαίνουν από το σχήμα, π.χ. το
(τα τελευταία βγαίνουν από το σχήμα, π.χ. το  είναι χαμηλότερα από το
είναι χαμηλότερα από το  και λοιπά). Άρα τα
και λοιπά). Άρα τα  είναι τα
είναι τα  που από την συνθήκη συνευθειακότητας των
που από την συνθήκη συνευθειακότητας των  έχουμε (κοιτάμε τις κλίσεις)
έχουμε (κοιτάμε τις κλίσεις)  , δηλαδή
, δηλαδή  .
.  το οποίο είναι
το οποίο είναι  με ισότητα όταν
με ισότητα όταν  (η ανισότητα ισοδυναμεί με τη
(η ανισότητα ισοδυναμεί με τη  ).
).  .
. , οπότε
, οπότε  .
. , που διέρχεται από το
, που διέρχεται από το  και τέμνει τους άξονες
και τέμνει τους άξονες  στα
στα  αντίστοιχα.
αντίστοιχα. πρέπει και αρκεί
πρέπει και αρκεί 

 .
. είναι σταθερό, το άθροισμά τους έχει ελάχιστο όταν γίνουν ίσοι (αν γίνεται, λόγω των περιορισμών).
είναι σταθερό, το άθροισμά τους έχει ελάχιστο όταν γίνουν ίσοι (αν γίνεται, λόγω των περιορισμών). , οπότε
, οπότε  , οπότε
, οπότε  .
.  , το δρόμο να περνά από τα
, το δρόμο να περνά από τα  . Το λευκό οικόπεδο θα έχει μέγιστο εμβαδόν ίσο με
. Το λευκό οικόπεδο θα έχει μέγιστο εμβαδόν ίσο με  .
. θα είναι
θα είναι 



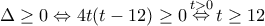
 οπότε
οπότε  όταν
όταν 
 οι προβολές του
οι προβολές του  στις
στις  ,
,  η προβολή του στην
η προβολή του στην  . Θέτω
. Θέτω 
 . Αλλά
. Αλλά 

 γίνεται :
γίνεται : 
 .
. σταθερό , το άθροισμα
σταθερό , το άθροισμα  γίνεται ελάχιστο όταν
γίνεται ελάχιστο όταν  .
. και άρα το υπόλοιπο του τετραγώνου θα είναι
και άρα το υπόλοιπο του τετραγώνου θα είναι 
 , γνωστή και απλή άσκηση .
, γνωστή και απλή άσκηση .  , (γνωστή κατασκευή)
, (γνωστή κατασκευή) προσδιορίζεται από τους άξονες και την εφαπτομένη της υπερβολής στο
προσδιορίζεται από τους άξονες και την εφαπτομένη της υπερβολής στο  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 11 επισκέπτες