Οικογένεια κύκλων

#1

: οικογένειες κύκλων.png (33.5 KiB) Προβλήθηκε 286 φορές

Να δειχθεί ότι η οικογένεια των κύκλων που διέρχονται από τα σημεία $A\left( {{x_1},{y_1}} \right)\,\,\kappa \alpha \iota \,\,B\left( {{x_2},{y_2}} \right)$ έχει την γενική μορφή:

$\left( {x - {x_1}} \right)\left( {x - {x_2}} \right) + \left( {y - {y_1}} \right)\left( {y - {y_2}} \right) + k\left( {ax + by + c} \right) = 0,\,\,k \in \mathbb{R}$

Όπου ax + by + c = 0

η ευθεία που ορίζουν τα $A\,\,\kappa \alpha \iota \,\,B$ .

Εφαρμογή : Να βρεθεί η εξίσωση του κύκλου που διέρχεται από τα σημεία , $A\left( {1,2} \right)\,\,,\,\,B\left( {3,4} \right)\,\,,\,\,C\left( {7,0} \right)$ .

#2

Doloros έγραψε: ↑
Πέμ Ιούλ 29, 2021 7:45 pm
οικογένειες κύκλων.png

Να δειχθεί ότι η οικογένεια των κύκλων που διέρχονται από τα σημεία $A\left( {{x_1},{y_1}} \right)\,\,\kappa \alpha \iota \,\,B\left( {{x_2},{y_2}} \right)$ έχει την γενική μορφή:

$\left( {x - {x_1}} \right)\left( {x - {x_2}} \right) + \left( {y - {y_1}} \right)\left( {y - {y_2}} \right) + k\left( {ax + by + c} \right) = 0,\,\,k \in \mathbb{R}$

Όπου η ευθεία που ορίζουν τα $A\,\,\kappa \alpha \iota \,\,B$ .

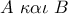Εφαρμογή : Να βρεθεί η εξίσωση του κύκλου που διέρχεται από τα σημεία , $A\left( {1,2} \right)\,\,,\,\,B\left( {3,4} \right)\,\,,\,\,C\left( {7,0} \right)$ .

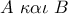Θέτοντας 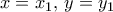$x=x_1,\, y=y_1$ βλέπουμε ότι ικανοποιείται η δοθείσα (άμεσο). Άρα το A(x_1,y_1)

είναι σημείο της. Όμοια το B(x_2,y_2)

. Eπίσης η δοθείσα γράφεται x^2+y^2+Ax+By+C=0

, που είναι εξίσωση κύκλου. Άρα είναι στην εν λόγω οικογένεια. Αντίστροφα:

Αν M(x,y)

βρίσκεται σε κάποιον από τους κύκλους, τότε η γωνία $\angle AMB$ είναι σταθερή για όλες τις θέσεις του

στον κύκλο αυτό. Ως προς κλίσεις, με αξιοποίηση των κλίσεων των MA,MB

που είναι $\displaystyle{ \frac {y-y_1} {x-x_1}, \, \frac {y-y_2} {x-x_2}}$ αυτό γράφεται

$\displaystyle{ \dfrac {\dfrac {y-y_1} {x-x_1}- \dfrac {y-y_2} {x-x_2} }{1+\dfrac {y-y_1} {x-x_1}\cdot \dfrac {y-y_2} {x-x_2} } = K}$

Διώχνοντας παρονομαστές και πολλαπλασιάζοντας χιαστί, γράφεται

$\displaystyle{ (y-y_1)(x-x_2)- (y-y_2)(x-x_1) = K\left ((x-x_1)(x-x_2)+ (y-y_1)(y-y_2) \right ) }$

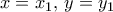To αριστερό μέλος γράφεται $\displaystyle{ x(y_2-y_1)+ y(x_1-x_2) - x_1y_2+x_2y_1}$ . Θέτοντας $x=x_1,\, y=y_1$ βλέπουμε ότι ισούται με

. Το ίδιο αν θέσουμε $x=x_2,\,y=y_2$ . Αρα η $\displaystyle{x(y_2-y_1)+ y(x_1-x_2) - x_1y_2+x_2y_1}$ , ως πρωτοβάθμια, είναι ευθεία που περιέχει τα A,B

. Αν την γράψουμε στην μορφή ax+by+c=0

καταλήγουμε στην ζητούμενη με k=-1/K

.

Εφαρμογή: Στα $A\left( {1,2} \right)\,\,,\,\,B\left( {3,4} \right)\,\,,\,\,C\left( {7,0} \right)$ δίνει με χρήση των δύο πρώτων

$\displaystyle{ (y-2)(x-3)- (y-4)(x-1) = K\left ((x-1)(x-3)+ (y-2)(y-4) \right ) }}$

Θέτοντας και τις συντεταγμένες του τρίτου σημείου, δηλαδή του C(7,0)

, παίρουμε

$\displaystyle{ (0-2)(7-3)- (0-4)(7-1) = K\left ((7-1)(7-3)+ (0-2)(0-4) \right ) }}$ από όπου K=1/2

. Άρα η ζητούμενη είναι η

$\displaystyle{ (x-1)(x-3)+ (y-2)(y-4) -2\left (- 2x+2y-2 \right )=0}$ , ισοδύναμα x^2+y^2-8x-2y+7=0

.

Edit: Διόρθωσα λογιστικό σφάλμα στο τέλος. Ευχαριστώ τον θεματοθέτη, φίλο Νίκο, που μου το επεσήμανε.

Οικογένεια κύκλων

Οικογένεια κύκλων

Re: Οικογένεια κύκλων

Μέλη σε σύνδεση