 είναι σημείο του επιπέδου και τα
είναι σημείο του επιπέδου και τα  σημεία των δύο αξόνων , ώστε :
σημεία των δύο αξόνων , ώστε : 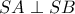 .
.Βρείτε τον γεωμετρικό τόπο του μέσου
 του τμήματος
του τμήματος  και το ελάχιστο του τμήματος
και το ελάχιστο του τμήματος  .
.Συντονιστής: Τηλέγραφος Κώστας
 είναι σημείο του επιπέδου και τα
είναι σημείο του επιπέδου και τα  σημεία των δύο αξόνων , ώστε :
σημεία των δύο αξόνων , ώστε : 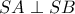 .
. του τμήματος
του τμήματος  και το ελάχιστο του τμήματος
και το ελάχιστο του τμήματος  .
.Ας το δούμε και με Αναλυτική Γεωμετρία, αν και η μέθοδος εδώ υστερεί της Γεωμετρικής. Είναι όμως διδακτική.
 οι συντεταγμένες του
οι συντεταγμένες του  τότε είναι
τότε είναι  . Η συνθήκη καθετότητας
. Η συνθήκη καθετότητας 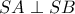 γίνεται
γίνεται  . Άρα
. Άρα  (ευθεία).
(ευθεία).
 , άρα
, άρα  , με ισότητα όταν
, με ισότητα όταν 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες