 και
και  επιλέξτε σημεία
επιλέξτε σημεία  , συνευθειακά
, συνευθειακάμε το
 , με
, με  και τέτοια ώστε :
και τέτοια ώστε :  .
.Συντονιστής: Τηλέγραφος Κώστας
 και
και  επιλέξτε σημεία
επιλέξτε σημεία  , συνευθειακά
, συνευθειακά , με
, με  και τέτοια ώστε :
και τέτοια ώστε :  .
. ενώ ,
ενώ ,
 έχω:
έχω:  και των
και των 
 . Θεωρώ
. Θεωρώ  .
. είναι ομόρροπα και άρα :
είναι ομόρροπα και άρα : οπότε
οπότε 
 είναι μέσο του
είναι μέσο του  και
και 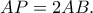 Η
Η  τέμνει την
τέμνει την  στο
στο  Φέρνω και το τμήμα
Φέρνω και το τμήμα  Με Π. Θ έχω
Με Π. Θ έχω  και
και  Με νόμο συνημιτόνου διαδοχικά στα τρίγωνα
Με νόμο συνημιτόνου διαδοχικά στα τρίγωνα 

 Αρκεί να δείξω ότι τα
Αρκεί να δείξω ότι τα  είναι συνευθειακά.
Μςνέλαος στο
είναι συνευθειακά.
Μςνέλαος στο  με διατέμνουσα
με διατέμνουσα 

 και με το αντίστροφο Μενελάου η
και με το αντίστροφο Μενελάου η  είναι διατέμνουσα του τριγώνου
είναι διατέμνουσα του τριγώνου και το ζητούμενο αποδείχτηκε.
και το ζητούμενο αποδείχτηκε. παράλληλη στην
παράλληλη στην  και τέμνει τις
και τέμνει τις  στα
στα  .
. έχει το
έχει το  μέσο της βάσης του
μέσο της βάσης του  και τα στοιχεία του είναι εύκολα προσδιόρισιμα .
και τα στοιχεία του είναι εύκολα προσδιόρισιμα . , θέτω επίσης :
, θέτω επίσης :  .
. με διατέμνουσα
με διατέμνουσα  έχω :
έχω : 
 . Αλλά στο
. Αλλά στο  η
η  είναι διχοτόμος και άρα:
είναι διχοτόμος και άρα:
 . Το σύστημα των
. Το σύστημα των  μας δίδει:
μας δίδει:  και τα
και τα  άμεσα προσδιορίζονται.
άμεσα προσδιορίζονται.
 και διατέμνουσες
και διατέμνουσες  αντίστοιχα έχω:
αντίστοιχα έχω:

 και
και 
 κι επειδή
κι επειδή  βρίσκω
βρίσκω  και αντικαθιστώντας στις παραπάνω σχέσεις παίρνω
και αντικαθιστώντας στις παραπάνω σχέσεις παίρνω  απ' όπου προκύπτει ότι το
απ' όπου προκύπτει ότι το  είναι μέσο του
είναι μέσο του  και το
και το  μέσο του
μέσο του 
Με
 κι έστω
κι έστω  επί της
επί της  με
με  και
και  .Είναι
.Είναι 
 είναι παραλ/μμο .Στο
είναι παραλ/μμο .Στο  με διατέμνουσα
με διατέμνουσα  ο Μενέλαος δίνει
ο Μενέλαος δίνει
 το 1ο θ.διαμέσου δίνει
το 1ο θ.διαμέσου δίνει  .
. μέσον της
μέσον της  άρα
άρα  και
και  εγγράψιμμο οπότε
εγγράψιμμο οπότε 
 είναι
είναι 
 είναι η τομή της
είναι η τομή της 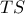 με την
με την  όπου
όπου  μέσον της
μέσον της 
 ,
,  που διέρχεται εκ του
που διέρχεται εκ του  .
. για την παραλλήλως τεταγμένη εφαπτομένη
για την παραλλήλως τεταγμένη εφαπτομένη  θα είναι
θα είναι


 ,
,  που διέρχεται από το
που διέρχεται από το  . Οι εστίες είναι τότε
. Οι εστίες είναι τότε  ,
,  .
. το (άνω) σημείο τομής της υπερβολής με τον κύκλο
το (άνω) σημείο τομής της υπερβολής με τον κύκλο  .
. προς την εφαπτομένη της υπερβολής στο
προς την εφαπτομένη της υπερβολής στο  προσδιορίζει τα σημεία
προσδιορίζει τα σημεία  ,
,  ,
, .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες