 του τεταρτοκυκλίου
του τεταρτοκυκλίου  , φέρουμε εφαπτομένη , η οποία τέμνει τις προεκτάσεις
, φέρουμε εφαπτομένη , η οποία τέμνει τις προεκτάσειςτων
 , στα σημεία
, στα σημεία  αντίστοιχα . Για ποια θέση του
αντίστοιχα . Για ποια θέση του  , προκύπτει :
, προκύπτει : 
Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
 του τεταρτοκυκλίου
του τεταρτοκυκλίου  , φέρουμε εφαπτομένη , η οποία τέμνει τις προεκτάσεις
, φέρουμε εφαπτομένη , η οποία τέμνει τις προεκτάσεις , στα σημεία
, στα σημεία  αντίστοιχα . Για ποια θέση του
αντίστοιχα . Για ποια θέση του  , προκύπτει :
, προκύπτει : 
Aν
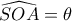 , η δοθείσα γράφεται
, η δοθείσα γράφεται 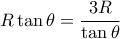 . Άρα
. Άρα  , οπότε
, οπότε  .
. , το
, το  είναι ύψος.
είναι ύψος.
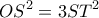 .
. 
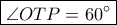 .
.Ας είναι λυμένο το πρόβλημα . Θέτω :
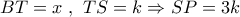 . Με
. Με  την ακτίνα του ημικυκλίου έχω :
την ακτίνα του ημικυκλίου έχω : . Άρα
. Άρα 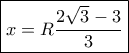 .
Αφού προσδιοριστεί το
.
Αφού προσδιοριστεί το  από την πιο πάνω , φέρνω εφαπτομένη του ημικυκλίου που διέρχεται από το
από την πιο πάνω , φέρνω εφαπτομένη του ημικυκλίου που διέρχεται από το  .
.Επειδή :
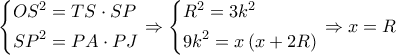 .
Δηλαδή στο ορθογώνιο
.
Δηλαδή στο ορθογώνιο 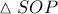 η
η 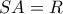 ( διάμεσος προς υποτείνουσα).
( διάμεσος προς υποτείνουσα).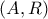 και θα κόψει το τεταρτοκύκλιο στο
και θα κόψει το τεταρτοκύκλιο στο  .
.Κατασκευάζουμε τo κοινό εφαπτόμενο τμήμα των κύκλων
 και
και 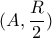 που
που  στο
στο  και την
και την  στο
στο  .Τότε,
.Τότε, (Η απόδειξη , απλή )
(Η απόδειξη , απλή )Παρόμοιο.
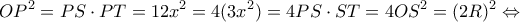
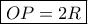
 φέρνω την εφαπτομένη του τεταρτοκυκλίου και προσδιορίζω το ζητούμενο σημείο
φέρνω την εφαπτομένη του τεταρτοκυκλίου και προσδιορίζω το ζητούμενο σημείο 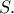
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες