 εφάπτεται στο ημικύκλιο και :
εφάπτεται στο ημικύκλιο και :  . Υπολογίστε το :
. Υπολογίστε το : 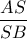
Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
Καθαρά εντός φακέλου (έχουμε και εκτός αλλά μετά την επόμενη λύση)
 το σημείο τομής της
το σημείο τομής της  με τον κύκλο
με τον κύκλο  . Τότε από το ορθογώνιο ισοσκελές τρίγωνο
. Τότε από το ορθογώνιο ισοσκελές τρίγωνο  είναι ο «βόρειος πόλος» του
είναι ο «βόρειος πόλος» του  (μιλάμε για πολύ κρύο ! εκεί
(μιλάμε για πολύ κρύο ! εκεί  ισοσκελές τραπέζιο (εγγεγραμμένο τραπέζιο σε κύκλο) οπότε το τρίγωνο
ισοσκελές τραπέζιο (εγγεγραμμένο τραπέζιο σε κύκλο) οπότε το τρίγωνο  είναι ισοσκελές άρα
είναι ισοσκελές άρα 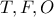 συνευθειακά, όπως φυσικά (λόγω των εφαπτομένων τμημάτων) και το τρίγωνο
συνευθειακά, όπως φυσικά (λόγω των εφαπτομένων τμημάτων) και το τρίγωνο 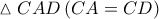 .
Από
.
Από 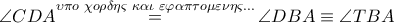 προκύπτει ότι τα ως άνω ισοσκελή τρίγωνα είναι όμοια, άρα
προκύπτει ότι τα ως άνω ισοσκελή τρίγωνα είναι όμοια, άρα  εγγράψιμο σε κύκλο και με
εγγράψιμο σε κύκλο και με  (
( διάμετρος του
διάμετρος του  ) θα είναι και
) θα είναι και 
 εγγράψιμο σε κύκλο , οπότε
εγγράψιμο σε κύκλο , οπότε 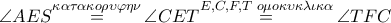
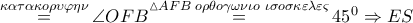 διέρχεται από τον «νότιο πόλο»
διέρχεται από τον «νότιο πόλο»  του
του  (εκεί να δεις ψόφο
(εκεί να δεις ψόφο 

Σχηματίζω το τετράγωνο
 . Τα τετράπλευρα
. Τα τετράπλευρα  είναι ισοσκελή τραπέζια .
είναι ισοσκελή τραπέζια . οι διαγώνιες του
οι διαγώνιες του  είναι ίσες με μέτρο την πλευρά του τετραγώνου , άρα η
είναι ίσες με μέτρο την πλευρά του τετραγώνου , άρα η 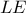 είναι κι αυτή εφαπτόμενο τμήμα στο ημικύκλιο .
είναι κι αυτή εφαπτόμενο τμήμα στο ημικύκλιο . και άρα η
και άρα η  είναι διχοτόμος του ορθογωνίου τριγώνου
είναι διχοτόμος του ορθογωνίου τριγώνου  .
. η τομή της
η τομή της  με αυτό , το
με αυτό , το  είναι ο νότιος πόλος του κύκλου .
είναι ο νότιος πόλος του κύκλου . είναι αρμονικό . Για κάθε σημείο
είναι αρμονικό . Για κάθε σημείο  του κύκλου η δέσμη:
του κύκλου η δέσμη: 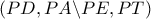 είναι αρμονική , άρα η δέσμη ,
είναι αρμονική , άρα η δέσμη ,  είναι αρμονική.
είναι αρμονική.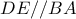 αν οι ευθείες
αν οι ευθείες  τέμνονται στο
τέμνονται στο  θα είναι :
θα είναι : 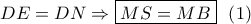 ( λόγω κεντρικής δέσμης ) .
( λόγω κεντρικής δέσμης ) . 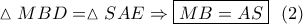
 έχω:
έχω: 
Έχω υποσχεθεί ακόμα μια λύση και δεν το ξεχνώ
 το σημείο τομής της υποτείνουσας του ορθογωνίου ισοσκελούς τριγώνου
το σημείο τομής της υποτείνουσας του ορθογωνίου ισοσκελούς τριγώνου  με τον κύκλο
με τον κύκλο  (προφανώς πρόκειται για τον βόρειο πόλο) και ας είναι
(προφανώς πρόκειται για τον βόρειο πόλο) και ας είναι 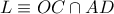 (προφανώς
(προφανώς  )
Προφανώς
)
Προφανώς  είναι το ορθόκεντρο του τριγώνου
είναι το ορθόκεντρο του τριγώνου (σημείο τομής δύο υψών του) λόγω
(σημείο τομής δύο υψών του) λόγω  διχοτόμος της
διχοτόμος της  χαρταετός και άρα
χαρταετός και άρα  , όπου
, όπου  .
.  είναι η ευθεία της συμμετροδιαμέσου του τριγώνου
είναι η ευθεία της συμμετροδιαμέσου του τριγώνου  διέρχεται από τον νότιο πόλο του
διέρχεται από τον νότιο πόλο του  (δηλαδή
(δηλαδή  μεσοκάθετη της
μεσοκάθετη της  , άρα αν
, άρα αν  τότε
τότε  είναι το μέσο της
είναι το μέσο της  και
και  το μέσο της
το μέσο της  (η διάμεσος του ορθογωνίου ισοσκελούς τριγώνου
(η διάμεσος του ορθογωνίου ισοσκελούς τριγώνου  και συνεπώς το
και συνεπώς το  είναι το βαρύκεντρο του εν λόγω τριγώνου (σημείο τομής δύο διαμέσων του) και άρα
είναι το βαρύκεντρο του εν λόγω τριγώνου (σημείο τομής δύο διαμέσων του) και άρα 
Σχηματίζω το τετράγωνο
 . Τα τετράπλευρα
. Τα τετράπλευρα  είναι ισοσκελή τραπέζια .
είναι ισοσκελή τραπέζια . οι διαγώνιες του
οι διαγώνιες του  είναι ίσες με μέτρο την πλευρά του τετραγώνου , άρα η
είναι ίσες με μέτρο την πλευρά του τετραγώνου , άρα η 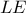 είναι κι αυτή εφαπτόμενο τμήμα στο ημικύκλιο .
είναι κι αυτή εφαπτόμενο τμήμα στο ημικύκλιο . και άρα η
και άρα η  είναι διχοτόμος του ορθογωνίου τριγώνου
είναι διχοτόμος του ορθογωνίου τριγώνου  .
. το μέσο του
το μέσο του  . Τα ορθογώνια τρίγωνα
. Τα ορθογώνια τρίγωνα  είναι προφανώς ίσα και άρα
είναι προφανώς ίσα και άρα  .
. έχω:
έχω: 
Έστω
 . Προφανώς
. Προφανώς  το ορθόκεντρο του τριγώνου
το ορθόκεντρο του τριγώνου  και συνεπώς
και συνεπώς 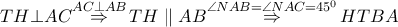 ισοσκελές τραπέζιο και ας είναι
ισοσκελές τραπέζιο και ας είναι  (το σημείο τομής των διαγωνίων του) είναι σημείο της μεσοκαθέτου των βάσεών του δηλαδή της
(το σημείο τομής των διαγωνίων του) είναι σημείο της μεσοκαθέτου των βάσεών του δηλαδή της  που είναι και η μεσοκάθετος της μιας βάσης το ισοσκελούς τραπεζίου
που είναι και η μεσοκάθετος της μιας βάσης το ισοσκελούς τραπεζίου  συνευθειακά .
συνευθειακά .  είναι το βαρύκεντρο του τριγώνου
είναι το βαρύκεντρο του τριγώνου  (σημείο τομής δύο διαμέσων του (των
(σημείο τομής δύο διαμέσων του (των  )) και συνεπώς η
)) και συνεπώς η  διέρχεται από το μέσο
διέρχεται από το μέσο  της
της  Στο ορθογώνιο τρίγωνο
Στο ορθογώνιο τρίγωνο  με ύψος προς την υποτείνουσά του το
με ύψος προς την υποτείνουσά του το 
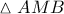 με διατέμνουσα την
με διατέμνουσα την  θα έχουμε:
θα έχουμε: 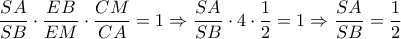
Με
 συμμετρικό του
συμμετρικό του  ως προς
ως προς  είναι
είναι 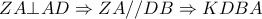 παραλ/μμο,άρα
παραλ/μμο,άρα 
 θα είναι
θα είναι  και
και 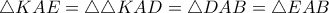

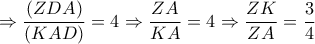



Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες