 πλευράς
πλευράς  και το ημικύκλιο διαμέτρου
και το ημικύκλιο διαμέτρου  εντός του τετραγώνου. Από το
εντός του τετραγώνου. Από το  φέρνω
φέρνω ευθεία που εφάπτεται του ημικυκλίου στο
 και τέμνει την
και τέμνει την  στο
στο 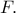 α) Να δείξετε ότι
α) Να δείξετε ότι 
β) Αν
 να βρείτε το εμβαδόν του τριγώνου
να βρείτε το εμβαδόν του τριγώνου 
Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
 πλευράς
πλευράς  και το ημικύκλιο διαμέτρου
και το ημικύκλιο διαμέτρου  εντός του τετραγώνου. Από το
εντός του τετραγώνου. Από το  φέρνω
φέρνω  και τέμνει την
και τέμνει την  στο
στο 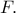 α) Να δείξετε ότι
α) Να δείξετε ότι 
 να βρείτε το εμβαδόν του τριγώνου
να βρείτε το εμβαδόν του τριγώνου 
Ας είναιgeorge visvikis έγραψε: ↑Κυρ Μάιος 08, 2022 7:43 pmΑριστεία στο τετράγωνο.png
Δίνεται τετράγωνοπλευράς
και το ημικύκλιο διαμέτρου
εντός του τετραγώνου. Από το
φέρνω
ευθεία που εφάπτεται του ημικυκλίου στοκαι τέμνει την
στο
α) Να δείξετε ότι
β) Αννα βρείτε το εμβαδόν του τριγώνου

 τότε και
τότε και 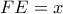 ( εφαπτόμενα τμήματα σε κύκλο). Για ίδιους λόγους
( εφαπτόμενα τμήματα σε κύκλο). Για ίδιους λόγους 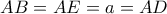 .
. ως προς τον κύκλο
ως προς τον κύκλο  θα έχω:
θα έχω: απ’ όπου,
απ’ όπου,  Τώρα θα έχω:
Τώρα θα έχω: 
 η προβολή του
η προβολή του  στην
στην  . Επειδή
. Επειδή  έτσι αν
έτσι αν  θα είναι
θα είναι  .
.
Είναιgeorge visvikis έγραψε: ↑Κυρ Μάιος 08, 2022 7:43 pmΑριστεία στο τετράγωνο.png
Δίνεται τετράγωνοπλευράς
και το ημικύκλιο διαμέτρου
εντός του τετραγώνου. Από το
φέρνω
ευθεία που εφάπτεται του ημικυκλίου στοκαι τέμνει την
στο
α) Να δείξετε ότι
β) Αννα βρείτε το εμβαδόν του τριγώνου

 άρα
άρα  και
και 

 άρα
άρα 

 ,
,  .
. ως οξείες με πλευρές κάθετες και ΑΟ διχοτόμος αφού ΒΑΕΟ χαρταετός. Άρα ο ζητούμενος λόγος είναι
ως οξείες με πλευρές κάθετες και ΑΟ διχοτόμος αφού ΒΑΕΟ χαρταετός. Άρα ο ζητούμενος λόγος είναι  .
. με πυθαγόρειο στο
με πυθαγόρειο στο  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες