 όπου
όπου  το έγκεντρο τριγώνου
το έγκεντρο τριγώνου  και
και  το σημείο τομής της διαμέσου
το σημείο τομής της διαμέσου  με την
με την 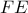 , με
, με  τα σημεία επαφής του έγκυκλου
τα σημεία επαφής του έγκυκλου  του
του  με τις πλευρές του
με τις πλευρές του  αντίστοιχα.
αντίστοιχα. Σημείωση: Πολύ πιθανόν να έχει ξανασυζητηθεί το θέμα στο
Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
 όπου
όπου  το έγκεντρο τριγώνου
το έγκεντρο τριγώνου  και
και  το σημείο τομής της διαμέσου
το σημείο τομής της διαμέσου  με την
με την 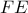 , με
, με  τα σημεία επαφής του έγκυκλου
τα σημεία επαφής του έγκυκλου  του
του  με τις πλευρές του
με τις πλευρές του  αντίστοιχα.
αντίστοιχα.  το σημείο επαφής του εγγεγραμμένου κύκλου με την
το σημείο επαφής του εγγεγραμμένου κύκλου με την  . Τότε, ορίζουμε το
. Τότε, ορίζουμε το  και θα δείξουμε ότι τα
και θα δείξουμε ότι τα  είναι συνευθειακά. Αφού
είναι συνευθειακά. Αφού  , θα έχουμε το ζητούμενο.
, θα έχουμε το ζητούμενο. στην
στην  τέμνει τις
τέμνει τις  στα
στα  . Είναι
. Είναι  , άρα τα
, άρα τα  είναι εγγράψιμα. Συνεπώς,
είναι εγγράψιμα. Συνεπώς,  , επομένως
, επομένως  , και αφού
, και αφού 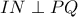 , προκύπτει
, προκύπτει  .
. είναι συνευθειακά, όποτε έχουμε το ζητούμενο.
είναι συνευθειακά, όποτε έχουμε το ζητούμενο. όπως και στον 1ο τρόπο. Είναι,
όπως και στον 1ο τρόπο. Είναι, 
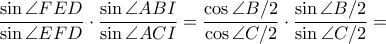

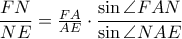 και αφού
και αφού  , προκύπτει
, προκύπτει  .
.  . Τότε,
. Τότε,  , οπότε το
, οπότε το 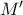 είναι το μέσον της
είναι το μέσον της  , όπως θέλαμε.
, όπως θέλαμε.ΈστωΣΤΑΘΗΣ ΚΟΥΤΡΑΣ έγραψε: ↑Πέμ Δεκ 23, 2021 2:37 pmκαθετότητα από το έγκεντρο.png
Να δειχτεί ότιόπου
το έγκεντρο τριγώνου
και
το σημείο τομής της διαμέσου
με την
, με
τα σημεία επαφής του έγκυκλου
του
με τις πλευρές του
αντίστοιχα.
Σημείωση: Πολύ πιθανόν να έχει ξανασυζητηθεί το θέμα στο
 και
και  οι ορθές προβολές των
οι ορθές προβολές των  στις
στις  αντίστοιχα. Τότε από
αντίστοιχα. Τότε από  προκύπτει ότι τα ορθογώνια τρίγωνα
προκύπτει ότι τα ορθογώνια τρίγωνα  είναι όμοια οπότε:
είναι όμοια οπότε:  οπότε από Stathis Koutras Theorem προκύπτει ότι
οπότε από Stathis Koutras Theorem προκύπτει ότι  και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες