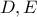 σημεία των πλευρών
σημεία των πλευρών  αντίστοιχα τριγώνου
αντίστοιχα τριγώνου  ώστε:
ώστε:  . Αν
. Αν  είναι τα σημεία τομής των μεσοκαθέτων των
είναι τα σημεία τομής των μεσοκαθέτων των  με τα τόξα
με τα τόξα  του περίκυκλου
του περίκυκλου  του τριγώνου
του τριγώνου  που δεν περιέχουν τα
που δεν περιέχουν τα  αντίστοιχα, να δείξετε ότι
αντίστοιχα, να δείξετε ότι 
Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
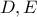 σημεία των πλευρών
σημεία των πλευρών  αντίστοιχα τριγώνου
αντίστοιχα τριγώνου  ώστε:
ώστε:  . Αν
. Αν  είναι τα σημεία τομής των μεσοκαθέτων των
είναι τα σημεία τομής των μεσοκαθέτων των  με τα τόξα
με τα τόξα  του περίκυκλου
του περίκυκλου  του τριγώνου
του τριγώνου  που δεν περιέχουν τα
που δεν περιέχουν τα  αντίστοιχα, να δείξετε ότι
αντίστοιχα, να δείξετε ότι 
 είναι τα μέσα των
είναι τα μέσα των  αντίστοιχα, τότε
αντίστοιχα, τότε  και όμοια
και όμοια  . Επομένως
. Επομένως  , οπότε αν
, οπότε αν  είναι το σημείο τομής των δύο μεσοκαθέτων, το περίκεντρο
είναι το σημείο τομής των δύο μεσοκαθέτων, το περίκεντρο  ισαπέχει από αυτές, οπότε ανήκει στην διχοτόμο της γωνίας τους. Επομένως το τρίγωνο
ισαπέχει από αυτές, οπότε ανήκει στην διχοτόμο της γωνίας τους. Επομένως το τρίγωνο  είναι ισοσκελές με πλευρές κάθετες προς εκείνες του επίσης ισοσκελούς
είναι ισοσκελές με πλευρές κάθετες προς εκείνες του επίσης ισοσκελούς 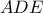 , οπότε έχουν παράλληλες τις διχοτόμους τους
, οπότε έχουν παράλληλες τις διχοτόμους τους  , άρα και οι βάσεις τους είναι παράλληλες, δηλαδή
, άρα και οι βάσεις τους είναι παράλληλες, δηλαδή  .
.Μπορείτε να απολαύσετε αυτή τη λύση. Πρόκειται για λύση ποίημα!!!!. Αντρέα σε ευχαριστώ θερμάAΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ έγραψε: ↑Τετ Δεκ 08, 2021 11:42 pmΑνείναι τα μέσα των
αντίστοιχα, τότε
και όμοια
. Επομένως NT=MS, οπότε αν
είναι το σημείο τομής των δύο μεσοκαθέτων, το περίκεντρο
ισαπέχει από αυτές, οπότε ανήκει στην διχοτόμο της γωνίας τους. Επομένως το τρίγωνο
είναι ισοσκελές με πλευρές κάθετες προς εκείνες του επίσης ισοσκελούς
, οπότε έχουν παράλληλες τις διχοτόμους τους
, άρα και οι βάσεις τους είναι παράλληλες, δηλαδή
.
Ας δούμε και μια άλλη άποψη , όχι βέβαια τόσο «μεστή» όπως του Αντρέα.ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ έγραψε: ↑Σάβ Δεκ 04, 2021 6:15 pmΠαραλληλία από μεσοκάθετες.png
Έστωσημεία των πλευρών
αντίστοιχα τριγώνου
ώστε:
. Αν
είναι τα σημεία τομής των μεσοκαθέτων των
με τα τόξα
του περίκυκλου
του τριγώνου
που δεν περιέχουν τα
αντίστοιχα, να δείξετε ότι

 είναι τα σημεία τομής των
είναι τα σημεία τομής των  με τον περίκυκλο του τριγώνου
με τον περίκυκλο του τριγώνου  , με
, με  τότε από τα ισοσκελή τρίγωνα
τότε από τα ισοσκελή τρίγωνα  (εξαιτίας των μεσοκαθέτων) προκύπτει ότι και τα τρίγωνα
(εξαιτίας των μεσοκαθέτων) προκύπτει ότι και τα τρίγωνα  είναι ισοσκελή και με
είναι ισοσκελή και με  προκύπτει ότι
προκύπτει ότι  είναι σημεία κύκλου με κέντρο
είναι σημεία κύκλου με κέντρο  . Έχουμε:
. Έχουμε:  και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί.Ας δούμε μία άλλη προσέγγιση που προέκυψε από την ανάγνωση της όμορφης απόδειξης του Ανδρέα πιο πάνω.ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ έγραψε: ↑Σάβ Δεκ 04, 2021 6:15 pmΈστωσημεία των πλευρών
αντίστοιχα τριγώνου
ώστε:
. Αν
είναι τα σημεία τομής των μεσοκαθέτων των
με τα τόξα
του περίκυκλου
του τριγώνου
που δεν περιέχουν τα
αντίστοιχα, να δείξετε ότι

 Έστω
Έστω  , τα μέσα των πλευρών
, τα μέσα των πλευρών  αντιστοίχως και
αντιστοίχως και  , τα μέσα των τμημάτων
, τα μέσα των τμημάτων  , αντιστοίχως.
, αντιστοίχως. και
και  και ας είναι
και ας είναι  η διχοτόμος της γωνίας
η διχοτόμος της γωνίας  , όπου
, όπου  είναι αντιστοίχως, ο περίκυκλος και το περίκεντρο του δοσμένου τριγώνου
είναι αντιστοίχως, ο περίκυκλος και το περίκεντρο του δοσμένου τριγώνου  .
. , όπου
, όπου  , είναι ορθογώνιο λόγω
, είναι ορθογώνιο λόγω 

 και
και 

 Ισχύει
Ισχύει  και ομοίως έχουμε
και ομοίως έχουμε 

 λόγω
λόγω  .
. τώρα, ως παράλληλες προς τις ακτίνες
τώρα, ως παράλληλες προς τις ακτίνες  αντιστοίχως, αποκόπτουν από τον κύκλο
αντιστοίχως, αποκόπτουν από τον κύκλο  ίσα τόξα λόγω της
ίσα τόξα λόγω της 



 και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. δεν προκύπτει από την ισότητα των τόξων
δεν προκύπτει από την ισότητα των τόξων  και μόνο, αλλά επιπροσθέτως και από το ότι οι ευθείες
και μόνο, αλλά επιπροσθέτως και από το ότι οι ευθείες  βρίσκονται προς το αυτό μέρος της γωνίας
βρίσκονται προς το αυτό μέρος της γωνίας  το κυρτό ή το μη κυρτό ( όπως στο ως άνω σχήμα ).
το κυρτό ή το μη κυρτό ( όπως στο ως άνω σχήμα ).Για να δούμε ....ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ έγραψε: ↑Σάβ Δεκ 04, 2021 6:15 pmΠαραλληλία από μεσοκάθετες.png
Έστωσημεία των πλευρών
αντίστοιχα τριγώνου
ώστε:
. Αν
είναι τα σημεία τομής των μεσοκαθέτων των
με τα τόξα
του περίκυκλου
του τριγώνου
που δεν περιέχουν τα
αντίστοιχα, να δείξετε ότι

 είναι το κέντρο του κύκλου που περνά από τα σημεία
είναι το κέντρο του κύκλου που περνά από τα σημεία  τότε,
τότε, 
 είναι σημείο του κύκλου
είναι σημείο του κύκλου  Το σημείο λοιπόν αυτό είναι το
Το σημείο λοιπόν αυτό είναι το  της άσκησης, όπως και το σημείο
της άσκησης, όπως και το σημείο 
 (
( μέσο του τόξου
μέσο του τόξου  ) τής γωνίας
) τής γωνίας  είναι κάθετη στο ευθύγραμμο τμήμα
είναι κάθετη στο ευθύγραμμο τμήμα 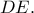 Παρατηρούμε ότι
Παρατηρούμε ότι 

 είναι οι τομές των κύκλων
είναι οι τομές των κύκλων 
 ενός τριγώνου
ενός τριγώνου  , τότε οι προβολές των σημείων τομής
, τότε οι προβολές των σημείων τομής 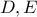 της ευθείας με τον περίκυκλο του τριγώνου, στις πλευρές
της ευθείας με τον περίκυκλο του τριγώνου, στις πλευρές  (έστω
(έστω  ) ισαπέχουν από τα μέσα
) ισαπέχουν από τα μέσα  των αντίστοιχων πλευρών, δηλαδή
των αντίστοιχων πλευρών, δηλαδή  . Αντίστροφα, αν
. Αντίστροφα, αν  τότε η ευθεία
τότε η ευθεία  είναι κάθετη στην διχοτόμο της
είναι κάθετη στην διχοτόμο της  .
. τα σημεία τομής των
τα σημεία τομής των  με τον περίκυκλο του
με τον περίκυκλο του  , τότε θα ισχύουν:
, τότε θα ισχύουν: (κατακορυφήν)
(κατακορυφήν) (από ισοσκελές)
(από ισοσκελές) (λόγω κύκλου), άρα
(λόγω κύκλου), άρα 

 άρα
άρα  εγγράψιμο.
εγγράψιμο. (από εγγράψιμο
(από εγγράψιμο  )
) (από εγγράψιμο
(από εγγράψιμο  ), δηλαδή έχουμε το ζητούμενο
), δηλαδή έχουμε το ζητούμενο 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες