 οι οποίες σχηματίζουν γωνία ίση με
οι οποίες σχηματίζουν γωνία ίση με 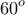 , κύκλος
, κύκλος 
επί του επιπέδου αυτών και σημείο
 επί του κύκλου αυτού. Να κατασκευαστεί ορθογώνιο τρίγωνο
επί του κύκλου αυτού. Να κατασκευαστεί ορθογώνιο τρίγωνο 
με
 ,
,  ,
,  και ακόμα να είναι:
και ακόμα να είναι:  .
.Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
 οι οποίες σχηματίζουν γωνία ίση με
οι οποίες σχηματίζουν γωνία ίση με 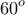 , κύκλος
, κύκλος 
 επί του κύκλου αυτού. Να κατασκευαστεί ορθογώνιο τρίγωνο
επί του κύκλου αυτού. Να κατασκευαστεί ορθογώνιο τρίγωνο 
 ,
,  ,
,  και ακόμα να είναι:
και ακόμα να είναι:  .
.Ανάλυση
 , μεταφέρω στην
, μεταφέρω στην  .
.  του
του  για το οποίο :
για το οποίο :  .
. γύρω από το
γύρω από το  κατά γωνία
κατά γωνία  και προκύπτει η ημιευθεία
και προκύπτει η ημιευθεία  , κάθετη στην
, κάθετη στην  στο
στο  που διέρχεται από το
που διέρχεται από το  .
. θα ανήκει σε ευθεία παράλληλη στην
θα ανήκει σε ευθεία παράλληλη στην  βάσει του πιο πάνω σταθερού λόγου .
βάσει του πιο πάνω σταθερού λόγου . γύρω από το σταθερό
γύρω από το σταθερό  κατά ορθή γωνία και προκύπτει η σταθερή
κατά ορθή γωνία και προκύπτει η σταθερή  , κάθετη στην
, κάθετη στην  στο σταθερό σημείο
στο σταθερό σημείο  .
. η σταθερή προβολή του
η σταθερή προβολή του  στην
στην  και
και  στην προέκταση της
στην προέκταση της 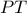 έτσι ώστε ,
έτσι ώστε ,  . Η κάθετη στην
. Η κάθετη στην  στο
στο  τέμνει την ευθεία
τέμνει την ευθεία  στο
στο  .
. ,
,  . Η κάθετη στην
. Η κάθετη στην  στο
στο  τέμνει την
τέμνει την  στο
στο  . Το
. Το  είναι αυτό που θέλω , βάσει της ανάλυσης .
είναι αυτό που θέλω , βάσει της ανάλυσης . μπορεί να αγνοηθεί . Μας αρκεί η (προσωρινά ας πούμε ) σταθερότητα του
μπορεί να αγνοηθεί . Μας αρκεί η (προσωρινά ας πούμε ) σταθερότητα του 
 .
.
 το έχω επιλέξει εντελώς ελεύθερο ( και όχι κατ' ανάγκη στο κύκλο).
το έχω επιλέξει εντελώς ελεύθερο ( και όχι κατ' ανάγκη στο κύκλο).  ,διαφορετική από το
,διαφορετική από το 
Νίκο καλημέρα από Γρεβενά..Doloros έγραψε: ↑Σάβ Δεκ 04, 2021 7:51 amΑνάλυση
Ας είναι λυμένο το πρόβλημα. Το σταθερό λόγο,, μεταφέρω στην
.
Δηλαδή θεωρώ σημείοτου
για το οποίο :
.
Στρέφω την οριζόντια ημιευθείαγύρω από το
κατά γωνία
και προκύπτει η ημιευθεία
, κάθετη στην
στο
που διέρχεται από το
.
Τοθα ανήκει σε ευθεία παράλληλη στην
βάσει του πιο πάνω σταθερού λόγου .
Κατασκευή .
Στρέφω τηνγύρω από το σταθερό
κατά ορθή γωνία και προκύπτει η σταθερή
, κάθετη στην
στο σταθερό σημείο
.
Ας είναιη σταθερή προβολή του
στην
και
στην προέκταση της
έτσι ώστε ,
. Η κάθετη στην
στο
τέμνει την ευθεία
στο
.
Θα είναι λόγω της,
. Η κάθετη στην
στο
τέμνει την
στο
. Το
είναι αυτό που θέλω , βάσει της ανάλυσης .
Το πρόβλημα έχει πάντα λύση .
Ο κύκλοςμπορεί να αγνοηθεί . Μας αρκεί η (προσωρινά ας πούμε ) σταθερότητα του

Το πρόβλημα λύνεται και με όμοιο τρόπο και για γωνία διαφορετική των.
Μπορούμε να μεταφέρουμε το σταθερό λόγο και στην άλλη ευθεία , δηλαδή στην
Παρατηρήσεις :
Στο παρακάτω δυναμικό αρχείο το σημείοτο έχω επιλέξει εντελώς ελεύθερο ( και όχι κατ' ανάγκη στο κύκλο).
Μπορείτε να το μετακινήσετε ελεύθερα και θα δείτε ότι υπάρχει μια λύση για κάθε θέση του,διαφορετική από το
.
Μέλη σε αυτήν τη Δ. Συζήτηση: Google [Bot] και 4 επισκέπτες