Εγγραφή τριγώνου σε τρεις κύκλους

#1

Δίνονται οι τρεις ομόκεντροι κύκλοι: $\displaystyle{C_1(O,2), C_2(O,7), C_3(O,9)}$ και σημείο $\displaystyle{A}$ επί του $\displaystyle{C_2}$ .
Να "εγγραφεί" σ' αυτούς ένα ορθογώνιο και ισοσκελές τρίγωνο.
Δηλαδή ένα τρίγωνο με κορυφή της ορθής γωνίας το δοσμένο σημείο $\displaystyle{A}$ και τις άλλες δύο κορυφές
στους άλλους δυο κύκλους αντίστοιχα.

: Κατασκευή τριγώνου 1.png (15.7 KiB) Προβλήθηκε 534 φορές

S.E.Louridas · #2

Η άρση της απόκρυψης μετά την επόμενη λύση:

Αν μου επιτρέπει ο Κώστας δίνω μία Ευκλείδεια Γεωμετρική αντίληψη:
Θεωρούμε σημείο

του κύκλου (C_2)

, και έστω το ζητούμενο ισοσκελές τρίγωνο ABC.

Θεωρούμε το ισοσκελές και ορθογώνιο τρίγωνο AOT.

Τα τρίγωνα AOB, ATC

προκύπτουν ίσα, άρα TC=OB, ct.

Οι τομές των κύκλων (T, OB), (O,R)

(

είναι η ακτίνα του κύκλου (C_3)

), αν υπάρχουν (διερεύνηση) δίνουν την κορυφή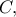

άρα και το ζητούμενο τρίγωνο

: κατ.png (69.92 KiB) Προβλήθηκε 427 φορές

edit: Μετά την λύση του Νίκου έκανα άρση της απόκρυψης, ώστε να φανεί και η ημέτερη λύση.

#3

KDORTSI έγραψε: ↑
Τρί Νοέμ 30, 2021 1:26 pm
Δίνονται οι τρεις ομόκεντροι κύκλοι: $\displaystyle{C_1(O,2), C_2(O,7), C_3(O,9)}$ και σημείο $\displaystyle{A}$ επί του $\displaystyle{C_2}$ .
Να "εγγραφεί" σ' αυτούς ένα ορθογώνιο και ισοσκελές τρίγωνο.
Δηλαδή ένα τρίγωνο με κορυφή της ορθής γωνίας το δοσμένο σημείο $\displaystyle{A}$ και τις άλλες δύο κορυφές
στους άλλους δυο κύκλους αντίστοιχα.

Κατασκευή τριγώνου 1.png

Κατασκευή

Με δεδομένο το

σημείο του $\left( {O,7} \right)$ φέρνω την

και τέμνει τον πιο μικρό κύκλο σε 2 σημεία , έστω το ένα απ’ αυτά

.

Κατασκευάζω το ορθογώνιο και ισοσκελές τρίγωνο $AOK\left( {\widehat {OAK} = 90^\circ } \right)$ ( ή το όμοιο του ζητούμενου εν γένει).

Η από το

παράλληλη προς την

τέμνει την

σε σημείο

. Γράφω τον κύκλο , $\left( {K,KP} \right)$ και τέμνει τον $\left( {O,9} \right)$ στο σημείο

.

Η κάθετη στην

στο

τέμνει τον $\left( {O,2} \right)$ στο

. Το $\vartriangle ABC$ είναι αυτό που θέλω.

: Εγγραφή τριγώνου σε τρείς κύκλους_oritzin_a.png (35.05 KiB) Προβλήθηκε 447 φορές

Απόδειξη

Τα τρίγωνα $AKC\,\,\kappa \alpha \iota \,\,AOB$ είναι ίσα . $(AK = AO\,\,,\,\,\widehat {KAC} = \widehat {OAB\,}\,\,,\,\,OD = KP = KC)$ και έμμεσο κριτήριο .

Από την προηγούμενη ισότητα έχω AB = AC

άρα το $\vartriangle ABC$ είναι ορθογώνιο και ισοσκελές .

Το πρόβλημα έχει $2\,\,,\,\,1$ ή καμιά λύση αν ο κύκλος $\left( {K,KP} \right)$ τέμνει εφάπτεται ή δεν έχει κοινό σημείο με τον κύκλο , $\left( {O,9} \right)$

: Εγγραφή τριγώνου σε τρείς κύκλους_oritzin_extra.png (19.41 KiB) Προβλήθηκε 439 φορές

Στο πιο πάνω σχήμα έχω επιλέξει την ακτίνα του μεσαίου κύκλου αντί , Για καλλίτερη εποπτεία.

nickchalkida · #4

Η κατασκευή μου δεν διαφέρει από αυτές των συναδέλφων, αλλά τη δίνω για την διατύπωση του ακόλουθου λήμματος.
Αν

,

σταθερά σημεία του επιπέδου, και το

περιστρέφεται περί του

στον σταθερό κύκλο (O,R)

,
κάθε σημείο

του επιπέδου τέτοιο ώστε

$\displaystyle{ {AC \over AB} = {k \over m} \ \ \ \& \ \ \ B\widehat{A}C = ct }$

θα διαγράφει επίσης κύκλο, κέντρου

και ακτίνας

, και θα είναι

$\displaystyle{ O\widehat{A}K = B\widehat{A}C \ \ \ \& \ \ \ AK = {k \over m}AO \ \ \ \& \ \ \ r = {k \over m}R }$

Επί της άσκησης, τα σημεία

,

του σχήματος προσδιορίζουν δύο λύσεις του προβλήματος δηλαδή δύο ορθογώνια, ισοσκελή τρίγωνα
(για οικονομία σχεδίασα μόνο το ένα)

S.E.Louridas · #5

KDORTSI έγραψε: ↑
Τρί Νοέμ 30, 2021 1:26 pm
Δίνονται οι τρεις ομόκεντροι κύκλοι: $\displaystyle{C_1(O,2), C_2(O,7), C_3(O,9)}$ και σημείο $\displaystyle{A}$ επί του $\displaystyle{C_2}$ .
Να "εγγραφεί" σ' αυτούς ένα ορθογώνιο και ισοσκελές τρίγωνο.
Δηλαδή ένα τρίγωνο με κορυφή της ορθής γωνίας το δοσμένο σημείο $\displaystyle{A}$ και τις άλλες δύο κορυφές
στους άλλους δυο κύκλους αντίστοιχα

Ας δούμε και μίας άλλης νοοτροπίας διαπραγμάτευση (αναγκαίος ο πλουραλισμός γαρ):

Θέλουμε την κατασκευή στο FIG.1.
Κατασκευάζουμε το σχήμα FIG.2, ως εξής:
Παίρνουμε ως βάση ένα ισοσκελές και ορθογώνιο τρίγωνο $( {\angle EDF = \frac{\pi }{2}}).$ Κατασκευάζουμε σημείο 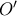έτσι ώστε $\displaystyle{\frac{{O'F}}{{O'D}} = \frac{{{R_3}}}{{{R_2}}}\;{{\kappa \alpha \iota }}\;\frac{{O'E}}{{O'F}} = \frac{{{R_1}}}{{{R_3}}},}$ ως τομή δύο Απολλώνιων κύκλων με βάσεις $DF,\;EF$ αντίστοιχα και αντίστοιχους λόγους $\displaystyle{\frac{{{R_3}}}{{{R_2}}}\;{{\kappa \alpha \iota }}\;\frac{{{R_1}}}{{{R_3}}}.}$ Έτσι έχουμε τον κατασκευαστικό προσδιορισμό των γωνιών $\displaystyle{\angle FO'D,\;\,\angle EO'D.}$ Μεταβαίνουμε τώρα στους δεδομένους κύκλους του FIG.1. και κατασκευάζουμε τις γωνίες $\displaystyle{\angle COA = \angle FO'D,$ και $\angle BOC = \angle EO'F.}$ Εύκολα τώρα, λόγω της ομοιότητας, προκύπτει ότι το τρίγωνο είναι ορθογώνιο και ισοσκελές με $\displaystyle{\angle BAC = \frac{\pi }{2}.}$

: kd.png (125.92 KiB) Προβλήθηκε 372 φορές

(*) Το πρόβλημα αυτό μπορεί να λυθεί για τρείς τυχόντες άνισους και ομόκεντρους κύκλους, όπου θα ζητείται η κατασκευή τριγώνου ABC

, όμοιου προς δοθέν, σε πλήρη δηλαδή γενίκευση. Μένει βέβαια για το δεδομένο πρόβλημα του εισηγητή και φίλτατου Κώστα, η αντιμετώπιση του με "Εργαλεία Καρτέσιου".

#6

Σωτήρη και Νίκο καθώς και nikhchalkida σας ευχαριστώ που ασχοληθήκατε με το θέμα αυτό
το οποίο είχε ως κεντρική ιδέα το μετασχηματισμό της στροφής.
Ο μετασχηματισμός αυτός είναι πολύ λειτουργικός σχεδόν σε όλα τα λογισμικά.
Είναι και πολύ εντυπωσιακός αν αξιοποιήσει κανείς και την κινητικότητα της όλης
διαδικασίας.
Θα μπορούσε κανείς να επεκτείνει το πρόβλημα αν αντί για κύκλους θεωρήσει ευθείες
ή ακόμα και άλλες γραμμές. Το θέμα γίνεται δυσκολότερο.
Έδωσα αριθμητικά δεδομένα για μια περίπτωση. Η διερεύνηση σε βάθος θα μπορούσε
να γίνει με αναλυτική μέθοδο.
Σωτήρη η δεύτερή σου ιδέα είναι όμορφη και αναρτώ το παρακάτω σχήμα για
"του λόγου το αληθές" και για τη συγκεκριμένη περίπτωση.

: Κατασκευεή 1.png (40.5 KiB) Προβλήθηκε 310 φορές

Υπενθύμιση: Το σημείο $\displaystyle{B}$ βρέθηκε από τη γωνία $\displaystyle{\omega}$ .

Να είστε καλά.

Κώστας Δόρτσιος

Εγγραφή τριγώνου σε τρεις κύκλους

Εγγραφή τριγώνου σε τρεις κύκλους

Re: Εγγραφή τριγώνου σε τρεις κύκλους

Re: Εγγραφή τριγώνου σε τρεις κύκλους

Re: Εγγραφή τριγώνου σε τρεις κύκλους

Re: Εγγραφή τριγώνου σε τρεις κύκλους

Re: Εγγραφή τριγώνου σε τρεις κύκλους

Μέλη σε σύνδεση