KDORTSI έγραψε: ↑Κυρ Νοέμ 28, 2021 11:20 pm
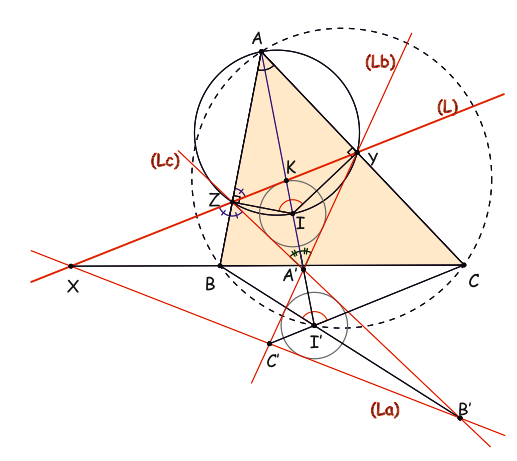
Δίνεται οξυγώνιο τρίγωνο

και ο περιγεγραμμένος του κύκλος

.
Επί του επιπέδου του τριγώνου αυτού χαράσσουμε ευθεία
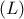
η οποία τέμνει τις πλευρές

και

αντίστοιχα στα σημεία

.
Στη συνέχεια χαράσσουμε τις συμμετρικές

της
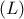
ως προς τις

.
Να δειχθεί ότι οι

ορίζουν ένα τρίγωνο του οποίου το έγκεντρο ανήκει στον κύκλο

.
(Πηγή: DIOFANTE.FR (Les récréations mathématiques))
- εγγεγραμμένος επί του περιγεγραμμένου.png (54.05 KiB) Προβλήθηκε 193 φορές
Έστω

και ομοίως κυκλικά τα σημεία

και έστω
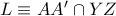
. Αν η κάθετη στην

στο σημείο

τέμνει την
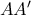
στο

τότε επειδή (λόγω της συμμετρίας )

διχοτόμος της

εξωτερικής του τριγώνου

η

θα είναι η εσωτερική διχοτόμος του τριγώνου και συνεπώς η σειρά
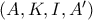
είναι αρμονική και άρα και η δέσμη

είναι αρμονική και με

της διχοτόμο (λόγω συμμετρίας) της
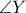
εξωτερικής του τριγώνου

η

θα είναι η εσωτερική διχοτόμος του εν λόγω τριγώνου οπότε
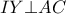
, άρα το τετράπλευρο
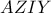
είναι εγγράψιμο σε κύκλο διαμέτρου

και το

είναι το έγκεντρο του τριγώνου

, οπότε η
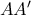
είναι διχοτόμος της

άρα και της κατακορυφήν της

. Ομοίως

είναι οι διχοτόμοι των γωνιών
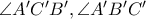
αντίστοιχα και ας είναι

το έγκενρτο του τριγώνου

. Τότε
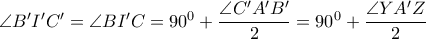

και συνεπώς
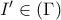
και το ζητούμενο έχει αποδειχθεί .
Στάθης και ο περιγεγραμμένος του κύκλος
και ο περιγεγραμμένος του κύκλος  .
. 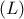 η οποία τέμνει τις πλευρές
η οποία τέμνει τις πλευρές  και
και  αντίστοιχα στα σημεία
αντίστοιχα στα σημεία  .
.  της
της 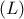 ως προς τις
ως προς τις  .
. ορίζουν ένα τρίγωνο του οποίου το έγκεντρο ανήκει στον κύκλο
ορίζουν ένα τρίγωνο του οποίου το έγκεντρο ανήκει στον κύκλο  .
.
 και ομοίως κυκλικά τα σημεία
και ομοίως κυκλικά τα σημεία  και έστω
και έστω 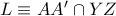 . Αν η κάθετη στην
. Αν η κάθετη στην  στο σημείο
στο σημείο  τέμνει την
τέμνει την 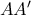 στο
στο  τότε επειδή (λόγω της συμμετρίας )
τότε επειδή (λόγω της συμμετρίας )  διχοτόμος της
διχοτόμος της  εξωτερικής του τριγώνου
εξωτερικής του τριγώνου  η
η  θα είναι η εσωτερική διχοτόμος του τριγώνου και συνεπώς η σειρά
θα είναι η εσωτερική διχοτόμος του τριγώνου και συνεπώς η σειρά 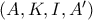 είναι αρμονική και άρα και η δέσμη
είναι αρμονική και άρα και η δέσμη  είναι αρμονική και με
είναι αρμονική και με  της διχοτόμο (λόγω συμμετρίας) της
της διχοτόμο (λόγω συμμετρίας) της 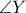 εξωτερικής του τριγώνου
εξωτερικής του τριγώνου  η
η  θα είναι η εσωτερική διχοτόμος του εν λόγω τριγώνου οπότε
θα είναι η εσωτερική διχοτόμος του εν λόγω τριγώνου οπότε 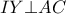 , άρα το τετράπλευρο
, άρα το τετράπλευρο 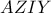 είναι εγγράψιμο σε κύκλο διαμέτρου
είναι εγγράψιμο σε κύκλο διαμέτρου  και το
και το  είναι το έγκεντρο του τριγώνου
είναι το έγκεντρο του τριγώνου  , οπότε η
, οπότε η  άρα και της κατακορυφήν της
άρα και της κατακορυφήν της  . Ομοίως
. Ομοίως  είναι οι διχοτόμοι των γωνιών
είναι οι διχοτόμοι των γωνιών 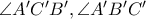 αντίστοιχα και ας είναι
αντίστοιχα και ας είναι  το έγκενρτο του τριγώνου
το έγκενρτο του τριγώνου  . Τότε
. Τότε 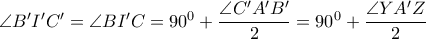
 και συνεπώς
και συνεπώς 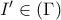 και το ζητούμενο έχει αποδειχθεί .
και το ζητούμενο έχει αποδειχθεί .