 , τριγώνου
, τριγώνου  , θεωρούμε σημείο
, θεωρούμε σημείο  και φέρουμε την κάθετη
και φέρουμε την κάθετη 
προς την
 , η οποία τέμνει την
, η οποία τέμνει την  στο σημείο
στο σημείο  . Αν :
. Αν :  , υπολογίστε το
, υπολογίστε το  ,
, συναρτήσει των πλευρών του
 . Εφαρμογή για :
. Εφαρμογή για :  .
.Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
 , τριγώνου
, τριγώνου  , θεωρούμε σημείο
, θεωρούμε σημείο  και φέρουμε την κάθετη
και φέρουμε την κάθετη 
 , η οποία τέμνει την
, η οποία τέμνει την  στο σημείο
στο σημείο  . Αν :
. Αν :  , υπολογίστε το
, υπολογίστε το  ,
,  . Εφαρμογή για :
. Εφαρμογή για :  .
. είναι οξείες .
είναι οξείες . και την από το
και την από το  παράλληλη στην
παράλληλη στην  που τέμνει την
που τέμνει την  στο
στο  .
. . Θ ισχύουν:
. Θ ισχύουν: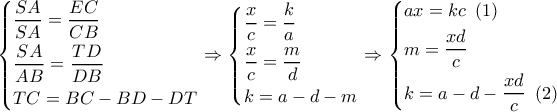
 λόγω της
λόγω της  δίδει:
δίδει:  .
.  οπότε:
οπότε:  .
. είναι αμβλεία εργάζομαι παρεμφερώς .
είναι αμβλεία εργάζομαι παρεμφερώς . και προκύπτει:
και προκύπτει: 
Στο σχήμα είναι
 οπότε
οπότε 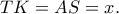


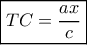 ,
,  και
και 
 Π. Θ στο
Π. Θ στο 


 και
και 
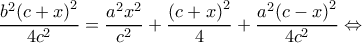


Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες