Εύκολη καθετότητα

#1

: Εύκολη καθετότητα.png (20.79 KiB) Προβλήθηκε 1342 φορές

Έστω κυρτό τετράπλευρο $\displaystyle{ABCD}$ με $\displaystyle{DA = AB = BC}$ και $\displaystyle{\angle A,\angle B}$ αμβλείες και ας είναι $\displaystyle{I}$ το σημείο τομής των διχοτόμων των γωνιών αυτών. Να δειχθεί ότι $\displaystyle{OI \bot CD}$ όπου $\displaystyle{O}$ το περίκεντρο του τριγώνου $\displaystyle{\vartriangle ABE}$ με $\displaystyle{E \equiv AD \cap BC}$

Στάθης

#2

ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ έγραψε: ↑
Δευ Ιαν 11, 2021 12:55 am
Εύκολη καθετότητα.pngΈστω κυρτό τετράπλευρο $\displaystyle{ABCD}$ με $\displaystyle{DA = AB = BC}$ και $\displaystyle{\angle A,\angle B}$ αμβλείες και ας είναι $\displaystyle{I}$ το σημείο τομής των διχοτόμων των γωνιών αυτών. Να δειχθεί ότι $\displaystyle{OI \bot CD}$ όπου $\displaystyle{O}$ το περίκεντρο του τριγώνου $\displaystyle{\vartriangle ABE}$ με $\displaystyle{E \equiv AD \cap BC}$

Στάθης

Καλημέρα Στάθη και Καλή Χρονιά!

Χωρίς βλάβη, υποθέτω ότι $\displaystyle B\widehat AD > A\widehat BC.$ Έστω M, N

τα μέσα των AB, AD

αντίστοιχα,

η προβολή του

στην

και

σημείο της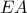

ώστε

Έστω ακόμα

το σημείο τομής των EI, KB.

Προφανώς το

είναι το

παράκεντρο του τριγώνου EAB

και η

διχοτομεί την $\widehat E.$

: Εύκολη καθετότητα.png (39.74 KiB) Προβλήθηκε 1275 φορές

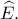Λόγω των ισοσκελών τριγώνων ABD, ABC,

εύκολα προκύπτει ότι τα τμήματα του ίδιου χρώματος είναι ίσα μεταξύ

τους, άρα και τα τρίγωνα IAD, ICB

οπότε $I\widehat DA=I\widehat BC$ και το EBID

είναι εγγράψιμο, ομοίως και το EAIC.

$\displaystyle MN|| = \frac{{BD}}{2}|| = HP \Leftrightarrow$ $\boxed{HN = PM = \frac{{KA}}{2}}$ (1)

$\displaystyle \left\{ \begin{array}{l} O{D^2} - {R^2} = AD \cdot DE\\ O{C^2} - {R^2} = CB \cdot CE \end{array} \right.\mathop \Rightarrow \limits^{CB = AD} O{D^2} - O{C^2} = AD(DE - CE) = AD(EA - EB) \Leftrightarrow$

$\displaystyle O{D^2} - O{C^2} = AD \cdot KA\mathop \Leftrightarrow \limits^{(1)} O{D^2} - O{C^2} = 2AD \cdot HN = I{D^2} - I{A^2} = I{D^2} - I{C^2}$

που αποδεικνύει το ζητούμενο (συνθήκη καθετότητας).

Δεν μου φάνηκε και τόσο απλή η καθετότητα, εκτός αν πήρα λάθος δρόμο

#3

george visvikis έγραψε: ↑
Δευ Ιαν 11, 2021 12:37 pm

ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ έγραψε: ↑
Δευ Ιαν 11, 2021 12:55 am
Εύκολη καθετότητα.pngΈστω κυρτό τετράπλευρο $\displaystyle{ABCD}$ με $\displaystyle{DA = AB = BC}$ και $\displaystyle{\angle A,\angle B}$ αμβλείες και ας είναι $\displaystyle{I}$ το σημείο τομής των διχοτόμων των γωνιών αυτών. Να δειχθεί ότι $\displaystyle{OI \bot CD}$ όπου $\displaystyle{O}$ το περίκεντρο του τριγώνου $\displaystyle{\vartriangle ABE}$ με $\displaystyle{E \equiv AD \cap BC}$

Στάθης
Καλημέρα Στάθη και Καλή Χρονιά!

...

Δεν μου φάνηκε και τόσο απλή η καθετότητα, εκτός αν πήρα λάθος δρόμο

Καλημέρα Γιώργο και καλή χρονιά επίσης!. Εύχομαι σε όλο τον κόσμο υγεία, υγεία , υγεία

Προφανώς και δεν πήρες λάθος δρόμο γιατί αλλιώς δεν θα έφτανες στο προορισμό σου. Απλά πήρες έναν δρόμο...
Θα περιμένω κάποιες πιθανές απαντήσεις ακόμα και θα δικαιολογήσω απόλυτα τον τίτλο (εύκολη καθετότητα) του προβλήματος

Με εκτίμηση
Στάθης

ΦΩΤΙΑΔΗΣ ΠΡΟΔΡΟΜΟΣ · #4

ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ έγραψε: ↑
Δευ Ιαν 11, 2021 12:55 am
Εύκολη καθετότητα.pngΈστω κυρτό τετράπλευρο $\displaystyle{ABCD}$ με $\displaystyle{DA = AB = BC}$ και $\displaystyle{\angle A,\angle B}$ αμβλείες και ας είναι $\displaystyle{I}$ το σημείο τομής των διχοτόμων των γωνιών αυτών. Να δειχθεί ότι $\displaystyle{OI \bot CD}$ όπου $\displaystyle{O}$ το περίκεντρο του τριγώνου $\displaystyle{\vartriangle ABE}$ με $\displaystyle{E \equiv AD \cap BC}$

Στάθης

Από το θεώρημα Στάθη Κούτρα αρκεί να δείξω ότι $ED\cdot O_1I_1=EC\cdot O_2I_2$ όπου O_1,O_2

οι προβολές του

στις

αντίστοιχα, όμοια ορίζονται I_1,I_2

.
Είναι $ED\cdot O_1I_1=(AE+AB)(AE/2+AI_1)=(AE+AB)(AE/2+s-AE)$ όπου

η ημιπερίμετρος του EAB

.
Αρκεί το (AE+AB)(s-AE/2)

να είναι συμμετρικό προς AE,BE

Πράγματι $..=(AE+AB)\cdot\dfrac{AB+BE}{2}$ άρα τελειώσαμε.

Al.Koutsouridis · #5

ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ έγραψε: ↑
Δευ Ιαν 11, 2021 12:55 am
Εύκολη καθετότητα.pngΈστω κυρτό τετράπλευρο $\displaystyle{ABCD}$ με $\displaystyle{DA = AB = BC}$ και $\displaystyle{\angle A,\angle B}$ αμβλείες και ας είναι $\displaystyle{I}$ το σημείο τομής των διχοτόμων των γωνιών αυτών. Να δειχθεί ότι $\displaystyle{OI \bot CD}$ όπου $\displaystyle{O}$ το περίκεντρο του τριγώνου $\displaystyle{\vartriangle ABE}$ με $\displaystyle{E \equiv AD \cap BC}$

Στάθης

Έστω

οι προβολές του

στις

αντίστοιχα και M,N

του

. Από το θεώρημα "Στάθης Κούτρας" αρκεί να δείξουμε ότι

$\dfrac{MA+AK}{NB+BL} = \dfrac{EC}{ED} \Leftrightarrow \dfrac{EA/2+MA}{EB/2+BL} = \dfrac{EB+BC}{EA+AD} \Leftrightarrow \dfrac{EA+2AM}{EB+2BL} = \dfrac{EB+BC}{EA+AD} \Leftrightarrow$

$\dfrac{EA+2AM+EB+2BL}{EB+2BL} = \dfrac{EB+EA+BC+AD}{EA+AD} \Leftrightarrow$

Όμως EA+2AM+EB+2BL = EB+EA+BC+AD

, οπότε

$EB+2BL=EA+AD \Leftrightarrow$

$EB+2BL =EA+AM+BL \Leftrightarrow$

EB+BL = EA+AM

Η τελευταία ισχύει επειδή το

είναι σημείο της διχοτόμου της γωνίας DEC

.

Edit: Με πρόλαβε ο Πρόδρομος ενω έγραφα, το αφήνω για τον κόπο...

giannimani · #6

: easy_perpend.png (108.57 KiB) Προβλήθηκε 1118 φορές

Από τον τρόπο του ορισμού του το σημείο

είναι το

παράκεντρο του $\vartriangle EAB$ .
Εφόσον DA=CB

σύμφωνα με το Λήμμα 1 ο κύκλος $\Omega \equiv (EAB)$ διέρχεται από το μέσο

του τόξου

του κύκλου $\omega_{1} \equiv (EDC)$ .

Έστω

,

τα μέσα των

,

αντίστοιχα. Τότε AP=BQ

και

, οπότε
σύμφωνα με τα Λήμματα

και

ο κύκλος $\omega_{2}\equiv (EAB)$ διέρχεται από το

και
από το

.

Συμβολίζουμε με

και

τα σημεία τομής της διχοτόμου

της γωνίας AEB

με τους κύκλους $\Omega$ και $\omega_{1}$ αντίστοιχα. Η

είναι εξωτερική διχοτόμος της
γωνίας AEB

, οπότε $\angle NEM= \angle NEL=90^{\circ}$ , και επομένως οι

,

διάμετροι
των κύκλων $\Omega$ , $\omega_{1}$ αντίστοιχα.

Θα αποδείξουμε ότι το σημείο

είναι το μέσο του

.

Έστω

το μέσο του

. Από την προφανή ομοιότητα των τριγώνων NAD

και

προκύπτει η ομοιότητα των τριγώνων NAP

και

, οπότε $\angle NPA=\angle NI'M$ ,
δηλαδή, $\angle NPE =\angle NI'E$ , από την οποία έχουμε ότι το μέσο

της

ανήκει
στον κύκλο $\omega_{2}$ . Αλλά και $I\in \omega_{2}$ , δηλαδή, $I' \equiv I$ .
Στο τρίγωνο MNL

τα

,

μέσα των

,

αντίστοιχα, οπότε $OI \parallel NL$ .
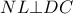Όμως $NL \bot DC$ , οπότε και $OI \bot DC$ .

Έγινε χρήση των δύο επόμενων λημμάτων (Οι αποδείξεις τους δεν παρουσιάζουν δυσκολίες).

Λημμα 1. Στις πλευρές

και

ενός σκαληνού τριγώνου ABC

,

, θεωρούμε
αντίστοιχα τα σημεία C_0

και

. Το σημείο B_1

είναι το μέσο του τόξου ABC

του περιγεγραμμένου κύκλου του τριγώνου ABC

.
Να αποδείξετε ότι η ισότητα AC_0 = CA_0

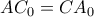ισχύει, αν και μόνο αν, τα σημεία
A_0

,

είναι ομοκυκλικά.

Λήμμα 2. Στις προεκτάσεις των πλευρών

και

(προς το μέρος των

και

) ενός σκαληνού
τριγώνου ABC

, θεωρούμε τα σημεία C_0

και

αντίστοιχα. Το σημείο $I_{b}$ είναι
το

παράκεντρο του τριγώνου ABC

. Να αποδείξετε ότι ο περιγεγραμμένος κύκλος
του τριγώνου $A_{0}BC_{0}$ , διέρχεται από το σημείο $I_{b}$ αν και μόνο αν AC_0 + CA_0 = AC

.

Al.Koutsouridis · #7

giannimani έγραψε: ↑
Παρ Ιαν 15, 2021 8:06 pm

Έγινε χρήση των δύο επόμενων λημμάτων (Οι αποδείξεις τους δεν παρουσιάζουν δυσκολίες).

Λημμα 1. Στις πλευρές και ενός σκαληνού τριγώνου , , θεωρούμε
αντίστοιχα τα σημεία και . Το σημείο είναι το μέσο του τόξου
του περιγεγραμμένου κύκλου του τριγώνου .
Να αποδείξετε ότι η ισότητα ισχύει, αν και μόνο αν, τα σημεία
, , , είναι ομοκυκλικά.

Λήμμα 2. Στις προεκτάσεις των πλευρών και (προς το μέρος των και ) ενός σκαληνού
τριγώνου , θεωρούμε τα σημεία και αντίστοιχα. Το σημείο $I_{b}$ είναι
το παράκεντρο του τριγώνου . Να αποδείξετε ότι ο περιγεγραμμένος κύκλος
του τριγώνου $A_{0}BC_{0}$ , διέρχεται από το σημείο $I_{b}$ αν και μόνο αν .

Την έψαχνα αυτή την λύση μολις είδα την εκφώνηση

. Το πρώτο λήμμα και το συγγενικό του δεύτερου.

Εύκολη καθετότητα

Εύκολη καθετότητα

Re: Εύκολη καθετότητα

Re: Εύκολη καθετότητα

Re: Εύκολη καθετότητα

Re: Εύκολη καθετότητα

Re: Εύκολη καθετότητα

Re: Εύκολη καθετότητα

Μέλη σε σύνδεση