 λέει
λέει Αν σε έναν κύκλο ακτίνας
 έχουμε δύο κάθετες χορδές
έχουμε δύο κάθετες χορδές  που τέμνονται στο
που τέμνονται στο  , τότε
, τότε  .
.H πρόταση και η απόδειξη είναι βέβαια γνωστά.
Ψάχνω πολλές αποδείξεις, από μαθητές και μη. Όταν τελειώσουμε, θα γράψω την απόδειξη του Αρχιμήδη.
Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
 λέει
λέει  έχουμε δύο κάθετες χορδές
έχουμε δύο κάθετες χορδές  που τέμνονται στο
που τέμνονται στο  , τότε
, τότε  .
. το κέντρο του κύκλου
το κέντρο του κύκλου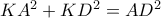
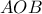 :
:




 προσθέτοντας τις
προσθέτοντας τις 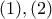 παίρνουμε
παίρνουμε 
Καλησπέρα σε όλους. Μια απάντηση με στοιχειώδη τριγωνομετρία.
 το κέντρο του κύκλου.
το κέντρο του κύκλου. , οπότε
, οπότε 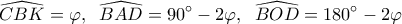
 κάθετη στη
κάθετη στη  , άρα
, άρα 
 είναι
είναι 
 είναι
είναι 

 είναι
είναι 
 .
. έχουμε
έχουμε  . Άρα
. Άρα 

Γεια σας. Ευχές στους εορτάζοντες των ημερών.Mihalis_Lambrou έγραψε: ↑Σάβ Ιαν 09, 2021 9:52 pmΣτο Περί Λημμάτων του Αρχιμήδη, ένα σχετικά μικρό κείμενο το οποίο σώζεται μόνο σε μεσαιωνική Αραβική μετάφραση, η Πρότασηλέει
Αν σε έναν κύκλο ακτίναςέχουμε δύο κάθετες χορδές
που τέμνονται στο
, τότε
.
H πρόταση και η απόδειξη είναι βέβαια γνωστά.
Ψάχνω πολλές αποδείξεις, από μαθητές και μη. Όταν τελειώσουμε, θα γράψω την απόδειξη του Αρχιμήδη.
 την ακτίνα του κύκλου έχουμε:
την ακτίνα του κύκλου έχουμε: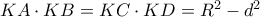


Μια άλλη ιδέα θα μπορούσε να είναι η ακόλουθη:Mihalis_Lambrou έγραψε: ↑Σάβ Ιαν 09, 2021 9:52 pmΣτο Περί Λημμάτων του Αρχιμήδη, ένα σχετικά μικρό κείμενο το οποίο σώζεται μόνο σε μεσαιωνική Αραβική μετάφραση, η Πρότασηλέει
Αν σε έναν κύκλο ακτίναςέχουμε δύο κάθετες χορδές
που τέμνονται στο
, τότε
.
H πρόταση και η απόδειξη είναι βέβαια γνωστά.
Ψάχνω πολλές αποδείξεις, από μαθητές και μη. Όταν τελειώσουμε, θα γράψω την απόδειξη του Αρχιμήδη.
 παράλληλη στην
παράλληλη στην  . Από το ισοσκελές τρπέζιο
. Από το ισοσκελές τρπέζιο  συμπεραίνουμε ότι το άθροισμα των τετραγώνων που μας ενδιαφέρεί είναι το άθροισμα των τερταγώνων των
συμπεραίνουμε ότι το άθροισμα των τετραγώνων που μας ενδιαφέρεί είναι το άθροισμα των τερταγώνων των  και
και  . Αλλά το
. Αλλά το  είναι ορθογώνιο στο
είναι ορθογώνιο στο  άρα η
άρα η  είναι διάμετρος και το αποδεικτέο έπεται.
είναι διάμετρος και το αποδεικτέο έπεται.
 τα μέσα των χορδών
τα μέσα των χορδών  .
.  το τετράπλευρο
το τετράπλευρο  είναι παραλληλόγραμμο , οπότε
είναι παραλληλόγραμμο , οπότε  . Θα ισχύουν ταυτόχρονα:
. Θα ισχύουν ταυτόχρονα:

 . Αντικαθιστώ στην
. Αντικαθιστώ στην  κι έχω το ζητούμενο .
κι έχω το ζητούμενο .Νίκο, κάνει με το παραπάνω. Δίνω άλλη λύση, την πρώτη της ξαδέλφη, αλλά με Αναλυτική Γεωμετρία. Το σχήμα είναι αυτό στο ποστ 7.nsmavrogiannis έγραψε: ↑Κυρ Ιαν 10, 2021 12:22 amΓεια σας. Ευχέ στους εορτάζοντες των ημερών.
Μιχάλη δεν ξέρω αν κάνει αυτή:
20120110.png
Μετην ακτίνα του κύκλου έχουμε:

 τα μέσα των
τα μέσα των  είναι τα
είναι τα 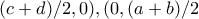 άρα το κέντρο
άρα το κέντρο  του κύκλου είναι το
του κύκλου είναι το  . Άρα με χρήση της
. Άρα με χρήση της  έχουμε
έχουμε 
 , που είναι το ζητούμενο.
, που είναι το ζητούμενο. και την κάθετο
και την κάθετο  . Εύκολα τώρα
. Εύκολα τώρα  και άρα
και άρα  Θυμομαστε ακόμα ότι
Θυμομαστε ακόμα ότι  (τεμνόμενες χορδές). Άρα
(τεμνόμενες χορδές). Άρα 
Mihalis_Lambrou έγραψε: ↑Σάβ Ιαν 09, 2021 9:52 pmΣτο Περί Λημμάτων του Αρχιμήδη, ένα σχετικά μικρό κείμενο το οποίο σώζεται μόνο σε μεσαιωνική Αραβική μετάφραση, η Πρότασηλέει
Αν σε έναν κύκλο ακτίναςέχουμε δύο κάθετες χορδές
που τέμνονται στο
, τότε
.
H πρόταση και η απόδειξη είναι βέβαια γνωστά.
Ψάχνω πολλές αποδείξεις, από μαθητές και μη. Όταν τελειώσουμε, θα γράψω την απόδειξη του Αρχιμήδη.
 (γνωστό θεώρημα για εγγεγραμμένο τετράπλευρο με κάθετες δαγώνιες)
(γνωστό θεώρημα για εγγεγραμμένο τετράπλευρο με κάθετες δαγώνιες)


 μέσα των
μέσα των  αντίστοιχα, άρα
αντίστοιχα, άρα  ορθογώνιο παραλληλόγραμμο, αφού
ορθογώνιο παραλληλόγραμμο, αφού  αποστήματα στις χορδές.
αποστήματα στις χορδές.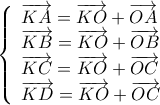 ,
, 
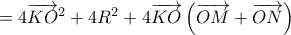

Θα δείξουμε ότι το περί ου ο λόγος άθροισμα τετραγώνων είναι σταθερό ανεξάρτητο από την θέση τουMihalis_Lambrou έγραψε: ↑Σάβ Ιαν 09, 2021 9:52 pmΣτο Περί Λημμάτων του Αρχιμήδη, ένα σχετικά μικρό κείμενο το οποίο σώζεται μόνο σε μεσαιωνική Αραβική μετάφραση, η Πρότασηλέει
Αν σε έναν κύκλο ακτίναςέχουμε δύο κάθετες χορδές
που τέμνονται στο
, τότε
.
H πρόταση και η απόδειξη είναι βέβαια γνωστά.
Ψάχνω πολλές αποδείξεις, από μαθητές και μη. Όταν τελειώσουμε, θα γράψω την απόδειξη του Αρχιμήδη.
 και επομένως ίσο με
και επομένως ίσο με 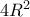 που προκύπτει αν πάρουμε την ειδική θέση του
που προκύπτει αν πάρουμε την ειδική θέση του  να συμπέσει με τo κέντρο του κύκλου. Για τον σκοπό αυτό αρκεί να δείξουμε ότι το άθροισμα αυτό δεν αλλάζει όταν μετακινήσουμε την μία από τις δύο χορδές ώστε να παραμέναι κάθεταη στην άλλη διότι με δύο τέτοιες μετακινήσεις το
να συμπέσει με τo κέντρο του κύκλου. Για τον σκοπό αυτό αρκεί να δείξουμε ότι το άθροισμα αυτό δεν αλλάζει όταν μετακινήσουμε την μία από τις δύο χορδές ώστε να παραμέναι κάθεταη στην άλλη διότι με δύο τέτοιες μετακινήσεις το  μπορεί να έλθει στην θέση του κέντρου. Ισοδύναμα αρκεί
μπορεί να έλθει στην θέση του κέντρου. Ισοδύναμα αρκεί 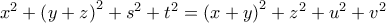



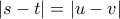
 )
)
 του "Περί Λημμάτων",
του "Περί Λημμάτων", 
Νίκο, χαίρομαι ιδιαίτερα για τα παραπάνω και ο λόγος είναι γιατί έχω μελετήσει πάρα πολύ καλά το Περί Λημμάτων αλλά δεν είχα δεί την συνάφεια των Προτάσεωνnickchalkida έγραψε: ↑Δευ Ιαν 11, 2021 6:53 amΆλλη μία, παραστατική, μη συμβατική απόδειξη, βασισμένη στην πρότασητου "Περί Λημμάτων",
 και
και  . Άλλωστε το Περί Λημμάτων δεν είναι κείμενο όπως ακριβώς το έγραψε ο Αρχιμήδης, αλλά έχει μικρές παραποιήσεις των μεταφραστών εδώ και εκεί (υπάρχει η άποψη ότι το κείμενο στα Αραβικά δίνει την εντύπωση πως είναι σημειώσεις μαθητή από μαθήματα που παρακολουθεί). Στο συγκεκριμένο σημείο οι
. Άλλωστε το Περί Λημμάτων δεν είναι κείμενο όπως ακριβώς το έγραψε ο Αρχιμήδης, αλλά έχει μικρές παραποιήσεις των μεταφραστών εδώ και εκεί (υπάρχει η άποψη ότι το κείμενο στα Αραβικά δίνει την εντύπωση πως είναι σημειώσεις μαθητή από μαθήματα που παρακολουθεί). Στο συγκεκριμένο σημείο οι  και
και  έπρεπε να είναι συνέχεια η μία της άλλης, χωρίς την παρεμβολή της άσχετης Πρότασης
έπρεπε να είναι συνέχεια η μία της άλλης, χωρίς την παρεμβολή της άσχετης Πρότασης  . Επίσης οι Προτάσεις
. Επίσης οι Προτάσεις  και
και  έχουν πολλά κοινά στοιχεία στην απόδειξη, που δεν υπάρχει λόγος να πει τα ίδια πράγματα δύο φορές ο Αρχιμήδη (άρα, πιθανότατα, κάποιος τα "πείραξε")
έχουν πολλά κοινά στοιχεία στην απόδειξη, που δεν υπάρχει λόγος να πει τα ίδια πράγματα δύο φορές ο Αρχιμήδη (άρα, πιθανότατα, κάποιος τα "πείραξε") .
.  οι χορδές
οι χορδές 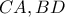 είναι κάθετες πλευρές ορθογωνίου τριγώνου (διότι αν φτιάξουμε με αυτές ένα τρίγωνο με κορυφές επί του κύκλου, τότε οι εγγεγραμμένες που τις βλέπουν έχουν άθροισμα
είναι κάθετες πλευρές ορθογωνίου τριγώνου (διότι αν φτιάξουμε με αυτές ένα τρίγωνο με κορυφές επί του κύκλου, τότε οι εγγεγραμμένες που τις βλέπουν έχουν άθροισμα  ). Του τριγώνου αυτού η υποτείνουσα είναι, βέβαια, διάμετρος.
). Του τριγώνου αυτού η υποτείνουσα είναι, βέβαια, διάμετρος.  )
)  , ο.ε.δ.
, ο.ε.δ.1.ΑνMihalis_Lambrou έγραψε: ↑Σάβ Ιαν 09, 2021 9:52 pmΣτο Περί Λημμάτων του Αρχιμήδη, ένα σχετικά μικρό κείμενο το οποίο σώζεται μόνο σε μεσαιωνική Αραβική μετάφραση, η Πρότασηλέει
Αν σε έναν κύκλο ακτίναςέχουμε δύο κάθετες χορδές
που τέμνονται στο
, τότε
.
H πρόταση και η απόδειξη είναι βέβαια γνωστά.
Ψάχνω πολλές αποδείξεις, από μαθητές και μη. Όταν τελειώσουμε, θα γράψω την απόδειξη του Αρχιμήδη.
 προφανώς
προφανώς  και ισχύει
και ισχύει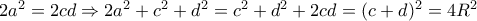
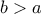 και
και  το συμμετρικό του
το συμμετρικό του  ως προς
ως προς  ,οπότε
,οπότε 
 ,συνεπώς ,
,συνεπώς ,  ισοσκελές τραπέζιο,άρα
ισοσκελές τραπέζιο,άρα 
 είναι εγγράψιμμο ,άρα
είναι εγγράψιμμο ,άρα  και ισχύει
και ισχύει
 ,άρα
,άρα 
 )
)Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες