Al.Koutsouridis έγραψε: ↑Κυρ Οκτ 18, 2020 12:15 am
Δίνονται τρεις θετικοί αριθμοί

, που ικανοποιούν τις συνθήκες

. Αποδείξτε με την σειρά τις προτάσεις:
1)

.
2) Υπάρχει ορθογώνιο τρίγωνο

το οποίο έχει υποτείνουσα

και κάθετη πλευρά

(βλ. σχήμα).
3) Ένα τρίγωνο

, στο οποίο

,

και η απόσταση

είναι ίση με

, θα έχει πλευρά

(βλ. σχήμα).
1) Η ανισότητα

προκύπτει εύκολα από τα δεδομένα της εκφώνησης, αφού

Για την ανισότητα
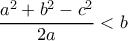
έχουμε ισοδύναμα
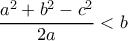

(εφόσον
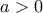
)


(εφόσον

)

Η τελευταία ισχύει από τα δεδομένα της εκφώνησης, άρα θα ισχύει και η αρχική.
2) Στο ερώτημα (1) αποδείχθηκε ότι

. Άρα θα ισχύει

. Επομένως θα υπάρχει το τρίγωνο

, κατασκευάζεται από την κάθετη πλευρά και την υποτείνουσα.
Κατασκευάζουμε τυχαίο κύκλο κέντου

και κατασκευάζουμε μια διάμετρό του. Διαλέγουμε τυχαίο σημείο

του κύκλου και κατασκευάζουμε ευθείες που διέρχονται από το σημείο

και τα άκρα της διαμέτρου. Οι ευθείες αυτές

είναι κάθετες. Πάνω στην ευθεία

κατακευάζουμε ευθύγραμμο τμήμα

μήκους

.
Με κέντρο το σημείο

κατακευάζουμε κύκλο ακτίνας

. Ο κύκλος αυτός θα τέμνει την ευθεία

σε δυο σημεία, αφού

. Έστω

ένα από αυτά. Τότε το τρίγωνο

είναι το ζητούμενο κατασκευαθέν.

- υπάρξεις1.png (11.36 KiB) Προβλήθηκε 612 φορές
3) Εννοείται ότι

. Στο τρίγωνο

από το νόμο των συνημιτόνων έχουμε

. Όμως

, οπότε



Άρα

.
 , που ικανοποιούν τις συνθήκες
, που ικανοποιούν τις συνθήκες  . Αποδείξτε με την σειρά τις προτάσεις:
. Αποδείξτε με την σειρά τις προτάσεις: .
. το οποίο έχει υποτείνουσα
το οποίο έχει υποτείνουσα  και κάθετη πλευρά
και κάθετη πλευρά  (βλ. σχήμα).
(βλ. σχήμα). , στο οποίο
, στο οποίο  ,
,  και η απόσταση
και η απόσταση  είναι ίση με
είναι ίση με  , θα έχει πλευρά
, θα έχει πλευρά  (βλ. σχήμα).
(βλ. σχήμα). , που ικανοποιούν τις συνθήκες
, που ικανοποιούν τις συνθήκες  . Αποδείξτε με την σειρά τις προτάσεις:
. Αποδείξτε με την σειρά τις προτάσεις: .
. το οποίο έχει υποτείνουσα
το οποίο έχει υποτείνουσα  και κάθετη πλευρά
και κάθετη πλευρά  (βλ. σχήμα).
(βλ. σχήμα). , στο οποίο
, στο οποίο  ,
,  και η απόσταση
και η απόσταση  είναι ίση με
είναι ίση με  , θα έχει πλευρά
, θα έχει πλευρά  (βλ. σχήμα).
(βλ. σχήμα). πλευρές τριγώνου και
πλευρές τριγώνου και 



 ισχύει
ισχύει  όπου
όπου 



 ) είναι
) είναι  με
με  ύψος
ύψος  λόγω της (1).
λόγω της (1).
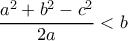 έχουμε ισοδύναμα
έχουμε ισοδύναμα (εφόσον
(εφόσον 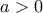 )
)
 (εφόσον
(εφόσον  )
)
 . Επομένως θα υπάρχει το τρίγωνο
. Επομένως θα υπάρχει το τρίγωνο  και κατασκευάζουμε μια διάμετρό του. Διαλέγουμε τυχαίο σημείο
και κατασκευάζουμε μια διάμετρό του. Διαλέγουμε τυχαίο σημείο  του κύκλου και κατασκευάζουμε ευθείες που διέρχονται από το σημείο
του κύκλου και κατασκευάζουμε ευθείες που διέρχονται από το σημείο  είναι κάθετες. Πάνω στην ευθεία
είναι κάθετες. Πάνω στην ευθεία  κατακευάζουμε ευθύγραμμο τμήμα
κατακευάζουμε ευθύγραμμο τμήμα  μήκους
μήκους  κατακευάζουμε κύκλο ακτίνας
κατακευάζουμε κύκλο ακτίνας  . Ο κύκλος αυτός θα τέμνει την ευθεία
. Ο κύκλος αυτός θα τέμνει την ευθεία  σε δυο σημεία, αφού
σε δυο σημεία, αφού  . Έστω
. Έστω  ένα από αυτά. Τότε το τρίγωνο
ένα από αυτά. Τότε το τρίγωνο  . Στο τρίγωνο
. Στο τρίγωνο  . Όμως
. Όμως  , οπότε
, οπότε

