 , του παραπάνω σχήματος, δίνονται:
, του παραπάνω σχήματος, δίνονται: και
και 
Να βρείτε το εμβαδόν της κυανής περιοχής.
Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
 , του παραπάνω σχήματος, δίνονται:
, του παραπάνω σχήματος, δίνονται: και
και 
 .
.  που είναι και εγγράψιμο στο κύκλο ακτίνας
που είναι και εγγράψιμο στο κύκλο ακτίνας  η γωνία
η γωνία  .
. η προβολή του
η προβολή του  στην
στην  , θα είναι
, θα είναι  .
. με εμβαδόν προφανώς ,
με εμβαδόν προφανώς , 

 είναι το μισό του εμβαδού του ορθογωνίου
είναι το μισό του εμβαδού του ορθογωνίου .
. , της πλευράς
, της πλευράς  )
) ( συμπληρώματα της γωνίας
( συμπληρώματα της γωνίας 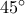 ) θα είναι :
) θα είναι : δηλαδή ισοδύναμα
δηλαδή ισοδύναμα  .
. άρα το ολικό που ζητάμε είναι
άρα το ολικό που ζητάμε είναι 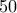
 στο σχήμα είναι ορθογώνιο και ισοσκελές.
στο σχήμα είναι ορθογώνιο και ισοσκελές. και τελικά ίσο με
και τελικά ίσο με  ..
..Καλησπέρα!Μιχάλης Νάννος έγραψε: ↑Πέμ Σεπ 24, 2020 6:20 pmshape.jpgΣτο ορθογώνιο, του παραπάνω σχήματος, δίνονται:
και
Να βρείτε το εμβαδόν της κυανής περιοχής.
 είναι το ζητούμενο εμβαδόν, τότε
είναι το ζητούμενο εμβαδόν, τότε 
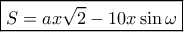
 Στο τρίγωνο
Στο τρίγωνο  είναι
είναι  Αλλά,
Αλλά, 

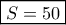

ΚαλησπέραΜιχάλης Νάννος έγραψε: ↑Πέμ Σεπ 24, 2020 6:20 pmshape.jpgΣτο ορθογώνιο, του παραπάνω σχήματος, δίνονται:
και
Να βρείτε το εμβαδόν της κυανής περιοχής.
 , ο Κύκλος
, ο Κύκλος  τέμνει το ορθογώνιο στα σημεία
τέμνει το ορθογώνιο στα σημεία 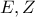




 που διέρχεται από τα
που διέρχεται από τα  . Είναι
. Είναι  .
. στο
στο  τέμνει την
τέμνει την 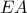 στο
στο  και τον κύκλο στο
και τον κύκλο στο  .Η
.Η  είναι διάμετρος και
είναι διάμετρος και  ,
, και
και  είναι ορθογώνια και ισοσκελή.
είναι ορθογώνια και ισοσκελή. 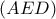 είναι το μισό του
είναι το μισό του  ενώ και
ενώ και  .
.  .
.  και
και  . Το
. Το  είναι και διάμεσος άρα
είναι και διάμεσος άρα  .
.  το
το  είναι το μέσον της
είναι το μέσον της  ενώ
ενώ  , άρα
, άρα  .
. .
.  οπότε και
οπότε και 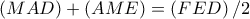 και αυτό που ζητάμε είναι είναι ίσο με
και αυτό που ζητάμε είναι είναι ίσο με  , δηλ. ίσο με
, δηλ. ίσο με 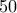 για
για  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες