Για την ισότητα των λόγων

Γιώργος Μήτσιος · #1

Χαίρετε!

: Για την ισότητα των λόγων.png (96.78 KiB) Προβλήθηκε 1128 φορές

Δίνεται το τετράγωνο ABCD

και $P \in AB$ ώστε να είναι $\dfrac{AB}{AP}=3$ .

Το ημικύκλιο διαμέτρου

τέμνει την

στο $E\not\equiv A$ . Να βρεθεί ο λόγος $\dfrac{AC}{EC}$

Ας επιτεθούμε στην άσκηση ...ποικιλοτρόπως! Σας ευχαριστώ, Γιώργος.

ΔΗΜΗΤΡΗΣ ΚΟΛΤΣΗΣ · #2

Γιώργος Μήτσιος έγραψε: ↑
Κυρ Αύγ 02, 2020 6:23 pm
Χαίρετε!
Για την ισότητα των λόγων.png
Δίνεται το τετράγωνο και $P \in AB$ ώστε να είναι $\dfrac{AB}{AP}=3$ .

Το ημικύκλιο διαμέτρου τέμνει την στο $E\not\equiv A$ . Να βρεθεί ο λόγος $\dfrac{AC}{EC}$

Ας επιτεθούμε στην άσκηση ...ποικιλοτρόπως! Σας ευχαριστώ, Γιώργος.

Καλησπέρα!

Έστω

η τομή της

με το ημικύκλιο διαμέτρου

.Θέτουμε

.
Τότε εύκολα έχουμε ότι το τετράπλευρο DSPA

είναι ορθογώνιο.
Άρα

$\frac{AB}{AP}=\frac{DC}{DS}=3\Rightarrow CS=\frac{2a}{3}$

Παίρνοντας τώρα τη δύναμη του σημείου

ως προς το ημικύκλιο έχουμε ότι

$CS\cdot CD=CE\cdot CA\Leftrightarrow...\Leftrightarrow CE=\frac{\sqrt{2}a}{3}$

Συνεπώς, $\frac{AC}{EC}=3$ .

#3

: για την ισότητα των λόγων.png (17.08 KiB) Προβλήθηκε 1089 φορές

Αν

το κέντρο του ημικυκλίου και αυτό , το ημικύκλιο, τέμνει την

ακόμα στο

, τότε η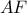

είναι κι αυτή διάμετρος του ημικυκλίου .

Συνεπώς : $\widehat {FEA} = 90^\circ$ . Αν οι $PF\,\,\kappa \alpha \iota \,\,AC$ διασταυρώνονται στο

αναγκαστικά το $\vartriangle FTC$ είναι ισοσκελές ορθογώνιο οπότε το

είναι μέσο

.

Αν

η προβολή του

στην

η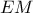

είναι διάμεσος του δισορθογωνίου τραπεζίου TPBC

και άρα $MB = MP \Rightarrow AP = PM = MB$ και άρα :

$AT = TE = EC \Rightarrow \boxed{\frac{{AC}}{{EC}} = 3}$

#4

: για την ισότητα των λόγων_new.png (20.62 KiB) Προβλήθηκε 1077 φορές

Έστω

το κέντρο του ημικυκλίου και

το σημείο τομής των ευθειών $DE\,\,\kappa \alpha \iota \,\,BC$

Επειδή $\widehat {{\xi _{}}} = 45^\circ \Rightarrow \widehat {EKD} = 2\widehat {{\xi _{}}} = 90^\circ$ , συνεπώς το

είναι μέσο του ημικυκλίου .

Το $\vartriangle DKE$ θα είναι αναγκαστικά ισοσκελές ορθογώνιο οπότε :

$\widehat {{\omega _{}}} + \widehat {{\theta _{}}} = 45^\circ \Rightarrow \dfrac{{\tan \omega + \tan \theta }}{{1 - \tan \omega \cdot \tan \theta }} = 1$ , κι αφού $\tan \theta = \dfrac{1}{3}$ προκύπτει : $\tan \omega = \dfrac{1}{2}$

Συνεπώς το

είναι μέσο του

και το

βαρύκεντρο του $\vartriangle DBC$ .

Έτσι από την προφανή αναλογία : $2 = \dfrac{{DE}}{{EM}} = \dfrac{{AE}}{{EC}} \Rightarrow \boxed{\dfrac{{AC}}{{EC}} = 3}$

#5

Γιώργος Μήτσιος έγραψε: ↑
Κυρ Αύγ 02, 2020 6:23 pm
Χαίρετε!
Για την ισότητα των λόγων.png
Δίνεται το τετράγωνο και $P \in AB$ ώστε να είναι $\dfrac{AB}{AP}=3$ .

Το ημικύκλιο διαμέτρου τέμνει την στο $E\not\equiv A$ . Να βρεθεί ο λόγος $\dfrac{AC}{EC}$

Ας επιτεθούμε στην άσκηση ...ποικιλοτρόπως! Σας ευχαριστώ, Γιώργος.

Καλημέρα!

: Για την ισότητα των λόγων.png (14.46 KiB) Προβλήθηκε 1059 φορές

Από το εγγεγραμμένο τετράπλευρο APED

εύκολα προκύπτουν οι γωνίες των $45^\circ.$ Με Π. Θ βρίσκω $\displaystyle DP = \frac{{a\sqrt {10} }}{3}$ και $\displaystyle DE = EP = \frac{{a\sqrt 5 }}{3}.$ Τέλος με Πτολεμαίο στο παραπάνω τετράπλευρο είναι:

$\displaystyle \frac{{a\sqrt 5 }}{3} \cdot a + \frac{{a\sqrt 5 }}{3} \cdot \frac{a}{3} = \frac{{a\sqrt {10} }}{3} \cdot AE \Leftrightarrow AE = \frac{{2a\sqrt 2 }}{3} = \frac{{2AC}}{3} \Leftrightarrow$ $\boxed{\dfrac{AC}{EC}=3}$

#6

Φέρνω $EK\bot AD$ και έστω DK=x,

οπότε

: Για την ισότητα των λόγων.β.png (16.78 KiB) Προβλήθηκε 1048 φορές

$\displaystyle {x^2} + {(a - x)^2} = D{E^2} = \frac{{5{a^2}}}{9} \Leftrightarrow {x^2} - ax + \frac{{2{a^2}}}{9} = 0\mathop \Leftrightarrow \limits^{2x < a} x = \frac{a}{3},$ άρα $\boxed{EC = \frac{{AC}}{3}}$

ksofsa · #7

Καλησπέρα!

Έστω

το κέντρο του τετραγώνου.

Το τρίγωνο DEP

ορθογώνιο ισοσκελές (προκύπτει από την εγγραψιμότητα του ADEP

).

Τα τρίγωνα ADP, ODE

όμοια , διότι ορθογώνια και

$\angle ADP=\angle ODE=45^{\circ}-\angle PDB$

Τελικά:

$\dfrac{OE}{OC}=\dfrac{OE}{OD}=\dfrac{AP}{AD}=\dfrac{1}{3}\Rightarrow \dfrac{CE}{OC}=\dfrac{2}{3}\Rightarrow \dfrac{CE}{AC}=\dfrac{1}{3}\Rightarrow \dfrac{AC}{CE}=3$

Μιχάλης Τσουρακάκης · #8

Γιώργος Μήτσιος έγραψε: ↑
Κυρ Αύγ 02, 2020 6:23 pm
Χαίρετε!
Για την ισότητα των λόγων.png
Δίνεται το τετράγωνο και $P \in AB$ ώστε να είναι $\dfrac{AB}{AP}=3$ .

Το ημικύκλιο διαμέτρου τέμνει την στο $E\not\equiv A$ . Να βρεθεί ο λόγος $\dfrac{AC}{EC}$

Ας επιτεθούμε στην άσκηση ...ποικιλοτρόπως! Σας ευχαριστώ, Γιώργος.

Έστω

μέσον της

. Λόγω ισότητας των πράσινων γωνιών θα είναι

$EZ \bot AB \Rightarrow HP//EZ//BC \Rightarrow AI=IE=EC \Rightarrow \dfrac{AC}{EC}=3$

: Ισότητα λόγων.png (9.73 KiB) Προβλήθηκε 979 φορές

p_gianno · #9

Γιώργος Μήτσιος έγραψε: ↑
Κυρ Αύγ 02, 2020 6:23 pm
Χαίρετε!
Για την ισότητα των λόγων.png
Δίνεται το τετράγωνο και $P \in AB$ ώστε να είναι $\dfrac{AB}{AP}=3$ .

Το ημικύκλιο διαμέτρου τέμνει την στο $E\not\equiv A$ . Να βρεθεί ο λόγος $\dfrac{AC}{EC}$

Ας επιτεθούμε στην άσκηση ...ποικιλοτρόπως! Σας ευχαριστώ, Γιώργος.

: λόγοι.PNG (42.4 KiB) Προβλήθηκε 909 φορές

Ο κύκλος διαμέτρου

διέρχεται από το σημείο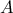

αφού

.

H

ως τμήμα της διαγωνίου του τετραγώνου διχοτομεί την γωνία DAP

άρα

(1)

Επίσης DE=EB

(2) (συμμετρία).

Από (1) και (2) έχουμε ότι τρίγωνο PEB

ισοσκελές και συνεπώς το ύψος του

θα διχοτομεί την

σε δύο κομμάτια 1/3 AB

το καθένα.

Είναι EK||CB

οπότε $\displaystyle \frac{AC}{CE}=\frac{AB}{KB}=\frac{3}{1}$

Γιώργος Μήτσιος · #10

Καλημέρα σε όλους! Δημήτρη, Νίκο, Γιώργο, Κώστα, Μιχάλη και Παναγιώτη σας ευχαριστώ για την..

..επιθετική σας διάθεση
και τον εμπλουτισμό του θέματος με κομψές λύσεις!
Μια παρόμοια, συνοπτικά και με βοηθό το σχήμα

: Για την ισότητα των λόγων B.png (83.16 KiB) Προβλήθηκε 869 φορές

Στο ορθόγώνιο και ισοσκελές $\triangle CEL$ το ύψος-διάμεσος $EH=\dfrac{CL}{2}=\dfrac{a}{3}$ , άρα $\dfrac{AC}{EC}=\dfrac{\left ( DAC \right )}{\left ( DEC \right )}=3$ .

Φιλικά, Γιώργος

#11

: Για την ισότητα των λόγων_Μήτσιος.png (28.18 KiB) Προβλήθηκε 843 φορές

Ας είναι

το σημείο τομής του ημικυκλίου με την

και

η τομή των $AC\,\,\kappa \alpha \iota \,\,SP$ .

Τα ισοσκελή ορθογώνια τρίγωνα $STC\,\,\,\kappa \alpha \iota \,\,\,PAT$ προφανώς έχουν : $TC = 2TA\,\,\left( 1 \right)$ .

Όμως στο $\vartriangle STC$ η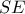

είναι ύψος άρα και διάμεσος ,οπότε : CE = ET

.

Αν λοιπόν θέσω $AT = m\,\,\,\kappa \alpha \iota \,\,\,TE = d$ λόγω της $\left( 1 \right)$ θα έχω :

$2d = 2m \Leftrightarrow d = m$ , δηλαδή: $AT = TE = EC \Rightarrow \boxed{\frac{{AC}}{{EC}} = 3}$

cool geometry · #12

$\angle DEP=90^{0}\Rightarrow \angle DAP+\angle DEP=180^{0}\Rightarrow \angle AEP=\angle ADP$
άρα $\cos \angle AEP=\cos \angle ADP=\frac{\sqrt{10}}{10},\sin \angle ADP=\frac{3\sqrt{10}}{10},\cos (45^{0}+\angle ADP)=\frac{2\sqrt{5}}{5} \Rightarrow \frac{\frac{a}{3}}{\frac{\sqrt{10}}{10}}=\frac{AE}{\frac{2\sqrt{5}}{5}}\Rightarrow AE=\frac{2\sqrt{2}}{3}a=\frac{2}{3}AC.$

Για την ισότητα των λόγων

Για την ισότητα των λόγων

Re: Για την ισότητα των λόγων

Re: Για την ισότητα των λόγων

Re: Για την ισότητα των λόγων

Re: Για την ισότητα των λόγων

Re: Για την ισότητα των λόγων

Re: Για την ισότητα των λόγων

Re: Για την ισότητα των λόγων

Re: Για την ισότητα των λόγων

Re: Για την ισότητα των λόγων

Re: Για την ισότητα των λόγων

Re: Για την ισότητα των λόγων

Μέλη σε σύνδεση