Καλησπέρα.
Στο παραπάνω σχήμα υπολογίστε το λόγο
 .
.Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
Καλησπέρα !Φανης Θεοφανιδης έγραψε: ↑Τετ Ιούλ 24, 2019 10:46 pm1.png
Καλησπέρα.
Στο παραπάνω σχήμα υπολογίστε το λόγο.
 το συμμετρικό του
το συμμετρικό του  ως προς το
ως προς το  και η διχοτόμος
και η διχοτόμος  της γωνίας
της γωνίας 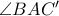 .
.
 άρα από θεώρημα διχοτόμων στο
άρα από θεώρημα διχοτόμων στο  αν
αν  τότε
τότε 
 είναι
είναι  άρα
άρα  και έτσι
και έτσι 
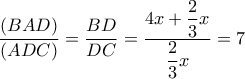
 . Κατασκευάζω τον Απολλώνιο κύκλο για κάθε
. Κατασκευάζω τον Απολλώνιο κύκλο για κάθε  του οποίου,
του οποίου, 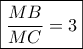 . Αν ο κύκλος αυτός κόψει το
. Αν ο κύκλος αυτός κόψει το  στο
στο  για κάθε
για κάθε  του κύκλου στο τρίγωνο
του κύκλου στο τρίγωνο  η
η  θα είναι διχοτόμος του .
θα είναι διχοτόμος του . και τέμνει τον κύκλο σε δύο σημεία . Έστω
και τέμνει τον κύκλο σε δύο σημεία . Έστω  το ένα απ’ αυτά . Το τρίγωνο
το ένα απ’ αυτά . Το τρίγωνο  προφανώς είναι το ζητούμενο .
προφανώς είναι το ζητούμενο .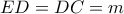 τότε:
τότε: 
 έχουμε:
έχουμε: 
 έχουμε
έχουμε
 πέρνουμε
πέρνουμε 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες