 το ύψος τριγώνου
το ύψος τριγώνου  και
και  οι προβολές του στις
οι προβολές του στις  αντίστοιχα.
αντίστοιχα. Αν
 είναι το περίκεντρο του τριγώνου, να δείξετε ότι
είναι το περίκεντρο του τριγώνου, να δείξετε ότι 
Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
 το ύψος τριγώνου
το ύψος τριγώνου  και
και  οι προβολές του στις
οι προβολές του στις  αντίστοιχα.
αντίστοιχα.  είναι το περίκεντρο του τριγώνου, να δείξετε ότι
είναι το περίκεντρο του τριγώνου, να δείξετε ότι 
Καλησπέρα Γιώργο.george visvikis έγραψε: ↑Σάβ Δεκ 22, 2018 7:23 pmΈστωτο ύψος τριγώνου
και
οι προβολές του στις
αντίστοιχα.
Ανείναι το περίκεντρο του τριγώνου, να δείξετε ότι

 , οπότε το
, οπότε το 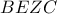 είναι εγγράψιμο. Οπότε,
είναι εγγράψιμο. Οπότε,  και
και  , συνεπώς από γνωστό Λήμμα,
, συνεπώς από γνωστό Λήμμα,  .
. .
. 
 είναι όμοια (αφού το
είναι όμοια (αφού το 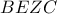 είναι εγγράψιμο), οπότε
είναι εγγράψιμο), οπότε  (1).
(1). (2).
(2). (3).
(3). (4).
(4). .
. , και το ζητούμενο αποδείχτηκε.
, και το ζητούμενο αποδείχτηκε. , οπότε αν
, οπότε αν  το αντιδιαμετρικό του
το αντιδιαμετρικό του  στον κύκλο
στον κύκλο 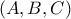 τα
τα  είναι συνευθειακά και ισχύει
είναι συνευθειακά και ισχύει  .
. , ή αλλιώς
, ή αλλιώς  .
. (το
(το 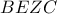 είναι εγγράψιμο και άρα τα
είναι εγγράψιμο και άρα τα  όμοια), οπότε αρκεί
όμοια), οπότε αρκεί  .
.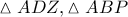 να είναι όμοια. Πράγματι:
να είναι όμοια. Πράγματι: (οι
(οι  είναι ισογώνιες, επομένως
είναι ισογώνιες, επομένως  )
)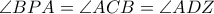
Ας είναιgeorge visvikis έγραψε: ↑Σάβ Δεκ 22, 2018 7:23 pmΤο μισό τρίγωνο.png
Έστωτο ύψος τριγώνου
και
οι προβολές του στις
αντίστοιχα.
Ανείναι το περίκεντρο του τριγώνου, να δείξετε ότι

 το αντιδιαμετρικό του
το αντιδιαμετρικό του  . Από το Θ. Ευκλείδη στα ορθογώνια τρίγωνα
. Από το Θ. Ευκλείδη στα ορθογώνια τρίγωνα  έχω :
έχω :  .
.  εγγράψιμο
εγγράψιμο  ,
,  ,
,  και
και  .
.  είναι δε γνωστά τα σύμβολα
είναι δε γνωστά τα σύμβολα  για τις
για τις  αντίστοιχα.
αντίστοιχα.
 είναι τυχαίο σημείο της
είναι τυχαίο σημείο της 
Γεια σου Γιώργο και καλά Χριστούγενναgeorge visvikis έγραψε: ↑Κυρ Δεκ 23, 2018 9:46 amΠολύ ωραίαΕυχαριστώ τον Ορέστη και τον Νίκο για τις απαντήσεις. Ας το γενικεύσουμε λιγάκι.
Εξετάστε αν συμβαίνει το ίδιο στην περίπτωση που τοείναι τυχαίο σημείο της

 με
με  . Επίσης, έστω
. Επίσης, έστω  και
και  .
. , οπότε αρκεί
, οπότε αρκεί  .
. , οπότε
, οπότε  , που δίνει
, που δίνει  .
.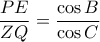 .
. , οπότε αρκεί
, οπότε αρκεί  ή ισοδύναμα
ή ισοδύναμα  (1).
(1). (αφού
(αφού  ) και
) και  (αφού
(αφού  ).
). , και η (1) αποδείχτηκε, οπότε τελειώσαμε.
, και η (1) αποδείχτηκε, οπότε τελειώσαμε.Καλά Χριστούγενναgeorge visvikis έγραψε: ↑Κυρ Δεκ 23, 2018 9:46 amΠολύ ωραίαΑς το γενικεύσουμε λιγάκι.
Εξετάστε αν συμβαίνει το ίδιο στην περίπτωση που τοείναι τυχαίο σημείο της

 και προφανώς
και προφανώς 


Την διάβασα, την απόλαυσα την,Μιχάλης Νάννος έγραψε: ↑Κυρ Δεκ 23, 2018 5:24 pmΚαλά Χριστούγενναgeorge visvikis έγραψε: ↑Κυρ Δεκ 23, 2018 9:46 amΠολύ ωραίαΑς το γενικεύσουμε λιγάκι.
Εξετάστε αν συμβαίνει το ίδιο στην περίπτωση που τοείναι τυχαίο σημείο της

shape.jpgΈστω
και προφανώς

Ισχύει:


Αλλιώς στο αρχικό πρόβλημα: Από το ισοσκελές τρίγωνοgeorge visvikis έγραψε: ↑Σάβ Δεκ 22, 2018 7:23 pmΤο μισό τρίγωνο.png
Έστωτο ύψος τριγώνου
και
οι προβολές του στις
αντίστοιχα.
Ανείναι το περίκεντρο του τριγώνου, να δείξετε ότι

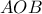 είναι (ως γνωστόν)
είναι (ως γνωστόν)  . Άρα
. Άρα  και όμοια
και όμοια  . Οπότε
. Οπότε 
 η
η  είναι διάμετρος οπότε
είναι διάμετρος οπότε  , ενώ από τον Ν.Ημιτόνων στο
, ενώ από τον Ν.Ημιτόνων στο  ισχύει
ισχύει  .
. . Έτσι έχουμε:
. Έτσι έχουμε: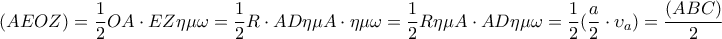 . Φιλικά , Γιώργος.
. Φιλικά , Γιώργος.


 .
. είναι
είναι 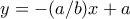 και οι συντεταγμένες του σημείου
και οι συντεταγμένες του σημείου  είναι
είναι 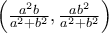 .
. είναι
είναι  και οι συντεταγμένες του σημείου
και οι συντεταγμένες του σημείου  είναι
είναι 

Δεν φαντάζομαι κάποιος τεμπέλης να καθόταν να έκανε όλες αυτές τις πράξεις πιο πιθανό ήταν να ψάξει βοηθητικές ευθείες ώστε να γράψει λιγότερα στην λύση, ή τουλάχιστον έτσι είμαι εγώΑνδρέας Πούλος έγραψε: ↑Παρ Ιαν 11, 2019 11:34 pmΜία λύση για "τεμπέλιδες" στη σκέψη είναι με Αναλυτική Γεωμετρία.
Ορίζουμε συντεταγμένες στο ορθοκανονικό σύστημα


.
Η εξίσωση της ευθείαςείναι
και οι συντεταγμένες του σημείου
είναι
.
Η εξίσωση της ευθείαςείναι
και οι συντεταγμένες του σημείου
είναι
Η εξίσωση του κύκλου που διέρχεται από τα σημεία A, B, C είναι
και από αυτή βρίσκουμε τις συντεταγμένες του κέντρου O.
Τώρα, το εμβαδον του τετραπλεύρου είναι άθροισμα των εμβαδών των τριγώνων (AEO) (AOZ) που υπολογίζονται από τον γνωστό τύπο.
Μέλη σε αυτήν τη Δ. Συζήτηση: ΛΕΚΚΑΣ ΓΙΩΡΓΟΣ και 4 επισκέπτες