Ας δούμε σε μετάφραση, μία από τις αποδείξεις που έχουν δημοσιευτεί
Εδώ.

Έστω

, το συμμετρικό σημείο του

ως προς την ευθεία

και έχουμε το ότι η ευθεία

περνάει από το σημείο

, λόγω

.
Έστω τα σημεία
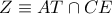
και

και
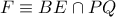
.
Στο τρίγωνο

με διατέμνουσα την ευθεία

, σύμφωνα με το
Θεώρημα Μενελάου, έχουμε
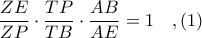
Από
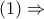


Από το πλήρες τετράπλευρο

έχουμε το ότι η σημειοσειρά

είναι αρμονική και επομένως, ισχύει


- Άθροισμα λόγων σε τρίγωνο.
- f22 t62879.png (19.21 KiB) Προβλήθηκε 482 φορές
Στο τρίγωνο

, λόγω της ως άνω αρμονικής σημειοσειράς, προκύπτει ότι η ευθεία

διχοτομεί την γωνία
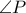
,
λόγω της

ως εξωτερικής διχοτόμου της γωνίας
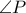
και άρα, έχουμε

Από


Από


Από
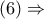

Από

και

και

λόγω συμμετρίας ως προς την ευθεία

, συμπεραίνεται ότι

και το ζητούμενο έχει αποδειχθεί.

Η απόδειξη αυτή είναι αφιερωμένη σε ένδειξη τιμής, στον θεματοδότη
Θάνο Καλογεράκη.
Κώστας Βήττας.
ΥΓ. Έχω το προνόμιο να με τιμά με την φιλία του ο
Θάνος Καλογεράκης, εραστής της Γεωμετρίας, λύτης και καταξιωμένος ήδη κατασκευαστής γεωμετρικών προβλημάτων, με διεθνή αναγνώριση.
Ο Θάνος ζει και δημιουργεί στο Κιάτο Κορινθίας, έχει τελειώσει το Ε.Μ.Π. και είναι Μηχανολόγος Μηχανικός εν ενεργεία. Έχει τρεις γιους που ακολουθούν τα χνάρια του πατέρα τους ως μελλοντικοί Μηχανικοί του Πολυτεχνείου.
Είμαι σίγουρος ότι έχει πολλά να μας προσφέρει τα επόμενα χρόνια και του εύχομαι ολόψυχα να χαίρεται τους ανθρώπους του, να έχει καλή υγεία και να συνεχίσει με τον ίδιο ενθουσιασμό να εμπνέεται ενδιαφέροντα γεωμετρικά προβλήματα.
 . Ας είναι
. Ας είναι  o "νότιος πόλος" του κύκλου διαμέτρου
o "νότιος πόλος" του κύκλου διαμέτρου 
 το σημείο τομής του κύκλου με την
το σημείο τομής του κύκλου με την  .
.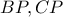 συναντούν τις
συναντούν τις  στα σημεία
στα σημεία 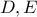 αντίστοιχα,
αντίστοιχα,

 και
και  ,άρα
,άρα 

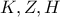 οι ορθές προβολές των
οι ορθές προβολές των  επί της
επί της 
 κι επειδή
κι επειδή  διχοτόμος της
διχοτόμος της 
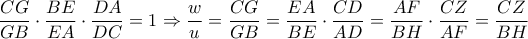
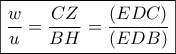 οπότε
οπότε 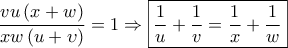

 Έστω
Έστω  , το συμμετρικό σημείο του
, το συμμετρικό σημείο του  ως προς την ευθεία
ως προς την ευθεία  περνάει από το σημείο
περνάει από το σημείο  .
.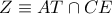 και
και  και
και 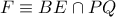 .
. με διατέμνουσα την ευθεία
με διατέμνουσα την ευθεία  , σύμφωνα με το
, σύμφωνα με το 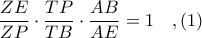
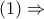

 έχουμε το ότι η σημειοσειρά
έχουμε το ότι η σημειοσειρά  είναι αρμονική και επομένως, ισχύει
είναι αρμονική και επομένως, ισχύει 
 διχοτομεί την γωνία
διχοτομεί την γωνία 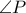 ,
,  ως εξωτερικής διχοτόμου της γωνίας
ως εξωτερικής διχοτόμου της γωνίας 




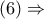

 και
και  και
και  λόγω συμμετρίας ως προς την ευθεία
λόγω συμμετρίας ως προς την ευθεία  και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί.