 εφάπτεται στις πλευρές
εφάπτεται στις πλευρές  στα σημεία
στα σημεία  αντίστοιχα.
αντίστοιχα. Έστω
 σημείο του τμήματος
σημείο του τμήματος  ώστε
ώστε  Να δείξετε ότι
Να δείξετε ότι 
Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
 εφάπτεται στις πλευρές
εφάπτεται στις πλευρές  στα σημεία
στα σημεία  αντίστοιχα.
αντίστοιχα.  σημείο του τμήματος
σημείο του τμήματος  ώστε
ώστε  Να δείξετε ότι
Να δείξετε ότι 
 ως παραπληρώματα ίσων γωνιών, αρκεί
ως παραπληρώματα ίσων γωνιών, αρκεί  (1).
(1). τέμνει την
τέμνει την  στο
στο  . Ξέρουμε πως οι
. Ξέρουμε πως οι  και
και  συντρέχουν στο σημείο
συντρέχουν στο σημείο  , έστω
, έστω  , άρα το τετράπλευρο
, άρα το τετράπλευρο  είναι πλήρες τετράπλευρο, δηλαδή οι διαγώνιες του τέμνονται αρμονικά. Με άλλα λόγια η τετράδα
είναι πλήρες τετράπλευρο, δηλαδή οι διαγώνιες του τέμνονται αρμονικά. Με άλλα λόγια η τετράδα  είναι αρμονική, άρα αφού
είναι αρμονική, άρα αφού  , από γνωστό λήμμα έχουμε πως η
, από γνωστό λήμμα έχουμε πως η  διχοτομεί την
διχοτομεί την  και άρα προκύπτει η (1).
και άρα προκύπτει η (1).Έστωgeorge visvikis έγραψε: ↑Δευ Ιούλ 23, 2018 10:31 amΊσες γωνίες.1.png
Ο έγκυκλος τριγώνουεφάπτεται στις πλευρές
στα σημεία
αντίστοιχα.
Έστωσημείο του τμήματος
ώστε
Να δείξετε ότι

 ,
,  τα ίχνη των καθέτων από τα σημεία
τα ίχνη των καθέτων από τα σημεία  ,
,  προς στις
προς στις  ,
,  αντίστοιχα. Παρατηρούμε ότι τα ορθογώνια τρίγωνα
αντίστοιχα. Παρατηρούμε ότι τα ορθογώνια τρίγωνα  ,
,  είναι όμοια μεταξύ τους. Επίσης όμοια μεταξύ τους είναι και τα
είναι όμοια μεταξύ τους. Επίσης όμοια μεταξύ τους είναι και τα  ,
,  . Απο τις παραπάνω ομοιότητες έχουμε
. Απο τις παραπάνω ομοιότητες έχουμε


 τα τρίγωνα
τα τρίγωνα  ,
,  είναι όμοια, δίνοντας την ζητούμνη ισότητα γωνιών.
είναι όμοια, δίνοντας την ζητούμνη ισότητα γωνιών. στην
στην  την τέμνει στο
την τέμνει στο  να δείξετε ότι το
να δείξετε ότι το  και τα μέσα
και τα μέσα  των
των  είναι συνευθειακά.
είναι συνευθειακά.Μια λύση "λίγο" εκτός φακέλουgeorge visvikis έγραψε: ↑Τρί Ιούλ 24, 2018 8:15 amΈνα επιπλέον ερώτημα... Ίσες γωνίες.1β.png
Αν η κάθετη από τοστην
την τέμνει στο
να δείξετε ότι το
και τα μέσα
των
είναι συνευθειακά.
 είναι συνευθειακά.
είναι συνευθειακά.  είναι ορθογώνιο. Άρα η
είναι ορθογώνιο. Άρα η  διχοτομείται από την
διχοτομείται από την  . Με άλλα λόγια αν
. Με άλλα λόγια αν  το μέσο του
το μέσο του  , τότε τα
, τότε τα  είναι συνευθειακά.
είναι συνευθειακά. είναι συνευθειακά.
είναι συνευθειακά. τέμνονται στο
τέμνονται στο  , το σημείο
, το σημείο  του τριγώνου ABC. Επομένως έχουμε το πλήρες τετράπλευρο
του τριγώνου ABC. Επομένως έχουμε το πλήρες τετράπλευρο  .
.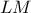 είναι η ευθεία
είναι η ευθεία  αυτού του πλήρους τετραπλεύρου. Επομένως αυτή η ευθεία διέρχεται από από το μέσο
αυτού του πλήρους τετραπλεύρου. Επομένως αυτή η ευθεία διέρχεται από από το μέσο  του
του 
 είναι συνευθειακά.
είναι συνευθειακά.  τα
τα  και
και  είναι μέσα, άρα έχουμε πως
είναι μέσα, άρα έχουμε πως  .
. .
. το μέσο του
το μέσο του  και
και  το συμμετρικό του
το συμμετρικό του  ως προς το
ως προς το  .
. είναι το σημείο
είναι το σημείο  του
του  , άρα προκύπτει από το θεώρημα
, άρα προκύπτει από το θεώρημα 
 είναι συνευθειακά.
είναι συνευθειακά.  και
και  μέσα στο
μέσα στο  , έχουμε πως
, έχουμε πως 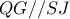 , άρα
, άρα  .
. , έχουμε πως τα τρίγωνα
, έχουμε πως τα τρίγωνα  και
και  είναι όμοια. Άρα και τα τρίγωνα που προκύπτουν από τις διαμέσους τους είναι όμοια, δηλαδή τα τρίγωνα
είναι όμοια. Άρα και τα τρίγωνα που προκύπτουν από τις διαμέσους τους είναι όμοια, δηλαδή τα τρίγωνα  και
και  είναι όμοια, άρα
είναι όμοια, άρα  , άρα προκύπτει η παραλληλία
, άρα προκύπτει η παραλληλία  και τέλος.
και τέλος. (έτσι το έχω ακούσει, αν και στο διαδίκτυο δεν υπάρχουν πολλά για αυτό):
(έτσι το έχω ακούσει, αν και στο διαδίκτυο δεν υπάρχουν πολλά για αυτό): και
και  το ύψος, το οποίο έχει μέσο
το ύψος, το οποίο έχει μέσο  . Έστω
. Έστω  το σημείο
το σημείο  και
και  το μέσο του
το μέσο του  . Τότε τα σημεία
. Τότε τα σημεία  είναι συνευθειακά!! Επιτέλους το χρησιμοποίησα αυτό το θεώρημα σε μία άσκηση
είναι συνευθειακά!! Επιτέλους το χρησιμοποίησα αυτό το θεώρημα σε μία άσκηση 'Εχουμε και λέμε:george visvikis έγραψε: ↑Δευ Ιούλ 23, 2018 10:31 amΊσες γωνίες.1.png Ο έγκυκλος τριγώνουεφάπτεται στις πλευρές
στα σημεία
αντίστοιχα.
Έστωσημείο του τμήματος
ώστε
Να δείξετε ότι
 οπότε αυτόματα παίρνουμε το ζητούμενο.
οπότε αυτόματα παίρνουμε το ζητούμενο.ΈστωΔιονύσιος Αδαμόπουλος έγραψε: ↑Τρί Ιούλ 24, 2018 3:07 pm----------------------
Θεώρημα(έτσι το έχω ακούσει, αν και στο διαδίκτυο δεν υπάρχουν πολλά για αυτό):
Έστω τρίγωνοκαι
το ύψος, το οποίο έχει μέσο
. Έστω
το σημείο
και
το μέσο του
. Τότε τα σημεία
είναι συνευθειακά!! Επιτέλους το χρησιμοποίησα αυτό το θεώρημα σε μία άσκηση



!
Υ.Γ Θα έχει ενδιαφέρον να δούμε μια απόδειξη αυτού του θεωρήματος. Έχω δει απόδειξη με μιγαδικούς, αλλά δεν έχω δει μια συνθετική λύση (χωρίς "αιρετικά" εργαλεία)
 Αν η
Αν η  τέμνει τη συμμετροδιάμεσο
τέμνει τη συμμετροδιάμεσο  στο
στο  θα δείξω ότι
θα δείξω ότι  είναι το σημείο
είναι το σημείο  Θεώρημα Μενελάου στο
Θεώρημα Μενελάου στο 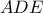 με διατέμνουσα
με διατέμνουσα 






 ο Θεώρημα διαμέσων στο
ο Θεώρημα διαμέσων στο 



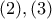 στην
στην  προκύπτει το ζητούμενο
προκύπτει το ζητούμενο 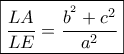
 (Η περίπτωση
(Η περίπτωση 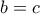 είναι προφανής).
είναι προφανής).Το είδα πρόσφατα εδώ, αλλά δεν ξέρω κατά πόσο έγκυρο είναι...george visvikis έγραψε: ↑Τετ Ιούλ 25, 2018 9:20 am
ΥΓ. Το θεώρημα το γνώριζα, την ονομασία όμως (θεώρημα Schlomich) πρώτη φορά την ακούω.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 20 επισκέπτες