Περίμετρος τριγώνου

Ιστοσελίδα · #1

: shape.png (27.25 KiB) Προβλήθηκε 615 φορές

Επί της διχοτόμου της γωνίας ABC

, εσωτερικά του τριγώνου $ABC\,({110^ \circ }{,20^ \circ }{,50^ \circ })$ , βρίσκεται σημείο

, τέτοιο ώστε $\angle DCA = {20^ \circ },\,\angle DCB = {30^ \circ }$ . Να δείξετε ότι η περίμετρος του τριγώνου ACD

ισούται με το μήκος του τμήματος

#2

Μιχάλης Νάννος έγραψε: ↑
Σάβ Δεκ 02, 2017 12:25 pm
shape.pngΕπί της διχοτόμου της γωνίας , εσωτερικά του τριγώνου $ABC\,({110^ \circ }{,20^ \circ }{,50^ \circ })$ , βρίσκεται σημείο , τέτοιο ώστε $\angle DCA = {20^ \circ },\,\angle DCB = {30^ \circ }$ . Να δείξετε ότι η περίμετρος του τριγώνου ισούται με το μήκος του τμήματος

Καλησπέρα Μιχάλη!

Στην προέκταση της

θεωρώ σημείο

ώστε

και έστω

η προβολή του

στην

Η

τέμνει την

στο

και η

στο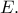

Οι γωνίες που φαίνονται στο σχήμα είναι προφανείς.

: Περίμετρος.png (21.42 KiB) Προβλήθηκε 573 φορές

Οι γωνίες $\widehat E_1, \widehat E_2$ έχουν το ίδιο ημίτονο και με νόμο ημιτόνων στα AEB, AEC,

είναι $\displaystyle \frac{{\sin ({{110}^0} - \omega )}}{{\sin \omega }} = \frac{{AC \cdot BE}}{{AB \cdot EC}}$

Ομοίως από νόμο ημιτόνων στα CED,CAD

και λόγω του θεωρήματος διχοτόμου είναι:

$\displaystyle \frac{{\sin {{30}^0}}}{{\sin {{20}^0}}} = \frac{{AC \cdot DE}}{{AD \cdot EC}} = \frac{{AC \cdot BE}}{{AB \cdot EC}} = \frac{{\sin ({{110}^0} - \omega )}}{{\sin \omega }} \Leftrightarrow \sin \omega = 2\sin {20^0}\sin ({110^0} - \omega ) \Leftrightarrow$

$\displaystyle \sin \omega = \cos ({90^0} - \omega ) - \cos ({130^0} - \omega ) \Leftrightarrow \sin \omega = \sin \omega - \cos ({130^0} - \omega )\mathop \Leftrightarrow \limits^{\omega < {{90}^0}}$ $\boxed{\omega=40^0}$

Τώρα εύκολα προκύπτει ότι $A\widehat EC=90^0,$ η

είναι διχοτόμος της $A\widehat DC$ και η

εξωτερική διχοτόμος, οπότε

το

είναι το

παράκεντρο του τριγώνου ADC

, άρα το

είναι ίσο με την ημιπερίμετρο του τριγώνου ADC.

Αλλά

οπότε $\displaystyle K\widehat HD = {30^0} \Leftrightarrow x = 2DK \Leftrightarrow$ $\boxed{x=AD+DC+AC}$

ΥΓ. Στην ουσία για την εύρεση της γωνίας $\omega$ έγινε απόδειξη του τριγωνομετρικού Ceva.

#3

Έστω τρίγωνο $\vartriangle ABC \to (110^\circ ,20^\circ ,50^\circ )$ και

το ύψος του . Πάνω στο

θεωρώ σημείο

τέτοιο ώστε : $\widehat {ACD} = 20^\circ \,\,\kappa \alpha \iota \,\,\widehat {DCK} = 30^\circ$ .

Θα δείξω πρώτα –πρώτα ότι η

διχοτομεί τη γωνία

του $\vartriangle ABC$ και έτσι το όλο σχήμα είναι αυτό της άσκησης .

Έστω

το συμμετρικό του

ως προς το

. Προφανώς το τρίγωνο DTC

είναι ισόπλευρο και το τετράπλευρο DBTC

είναι χαρταετός , άρα $\boxed{BD = BT}$ .

Γράφω τον κύκλο (D,DT)

τον οποίο η

τέμνει στο

. Είναι βεβαίως ισοσκελές το $\vartriangle DSC \to (140^\circ ,20^\circ \,,20^\circ )$ .

Στο $\vartriangle ASD$ η εξωτερική γωνία του στο

είναι $40^\circ$ συνεπώς κι αυτό είναι ισοσκελές της μορφής $(140^\circ ,20^\circ \,,20^\circ )$ .

Επειδή από κατασκευής $\widehat {BAD} = 70^\circ$ αναγκαστικά η

είναι ο φορέα της διχοτόμου στο τρίγωνο αυτό ( $\vartriangle ASD$ ) και το σημείο τομής

των

: περίμετρος_Nannou.png (61.6 KiB) Προβλήθηκε 559 φορές

$AB\,\,\kappa \alpha \iota \,\,DS\,\,$ είναι μέσο του

και το τετράπλευρο ASBD

είναι χαρταετός.

Επί πλέον αφού $OS = OT \Leftrightarrow \dfrac{{OS}}{2} = \dfrac{{OT}}{2} \Leftrightarrow \boxed{DM = DK}$ που μας εξασφαλίζει

ότι η

διχοτομεί τη γωνία

του $\vartriangle ABC$ . Έστω τώρα

το σημείο τομής των $SC\,\,\kappa \alpha \iota \,\,BT$ . Μετά απ’ αυτά :

$\widehat {BTC} = \widehat {BDC} = 180^\circ - 30^\circ - 10^\circ = 140^\circ \Rightarrow \boxed{\widehat {CTE} = 40}$ Αλλά και $\boxed{\widehat E = \widehat {EBS} = 40^\circ }$ που σημαίνει ότι $\boxed{CE = CT = CD}$

Αφού όμως $SB = ST \Leftrightarrow DB = SA + AC + CE \Leftrightarrow \boxed{DB = AD + AC + CD}$ .

Περίμετρος τριγώνου

Περίμετρος τριγώνου

Re: Περίμετρος τριγώνου

Re: Περίμετρος τριγώνου

Μέλη σε σύνδεση