 και σημείο του
και σημείο του  . Γράφω νέο κύκλο
. Γράφω νέο κύκλο 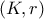 που τέμνει τον
που τέμνει τον προηγούμενο στα
 . Τέμνουσα διερχόμενη από το
. Τέμνουσα διερχόμενη από το  τέμνει τον κύκλο
τέμνει τον κύκλο 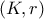
στο
 και τον κύκλο
και τον κύκλο  στο
στο  . Αν
. Αν  να υπολογιστούν οι
να υπολογιστούν οι πλευρές του
 .
.Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
 και σημείο του
και σημείο του  . Γράφω νέο κύκλο
. Γράφω νέο κύκλο 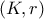 που τέμνει τον
που τέμνει τον  . Τέμνουσα διερχόμενη από το
. Τέμνουσα διερχόμενη από το  τέμνει τον κύκλο
τέμνει τον κύκλο 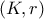
 και τον κύκλο
και τον κύκλο  στο
στο  . Αν
. Αν  να υπολογιστούν οι
να υπολογιστούν οι  .
.Για να μη μείνει αναπάντητη.Doloros έγραψε:Έστω κύκλοςκαι σημείο του
. Γράφω νέο κύκλο
που τέμνει τον
προηγούμενο στα. Τέμνουσα διερχόμενη από το
τέμνει τον κύκλο
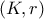
στοκαι τον κύκλο
στο
. Αν
να υπολογιστούν οι
πλευρές του.
 είναι εκατέρωθεν του
είναι εκατέρωθεν του 
 κι επειδή η
κι επειδή η  είναι διχοτόμος
είναι διχοτόμος το τρίγωνο
το τρίγωνο  είναι ισοσκελές, άρα
είναι ισοσκελές, άρα 


 και από τα όμοια τρίγωνα
και από τα όμοια τρίγωνα  είναι
είναι 

 από την
από την  και από
και από  καταλήγω στην εξίσωση:
καταλήγω στην εξίσωση: και από τη
και από τη  φαίνεται ότι έχουμε δύο τρίγωνα που επαληθεύουν
φαίνεται ότι έχουμε δύο τρίγωνα που επαληθεύουν  ή
ή 
 είναι εκατέρωθεν του
είναι εκατέρωθεν του 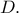 Θα επανέλθω σε επόμενη ανάρτηση...
Θα επανέλθω σε επόμενη ανάρτηση... είναι εκατέρωθεν του
είναι εκατέρωθεν του 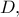 τότε έχουμε τα παρακάτω σχήματα.
Εργαζόμενοι όπως και προηγουμένως βρίσκουμε ότι
τότε έχουμε τα παρακάτω σχήματα.
Εργαζόμενοι όπως και προηγουμένως βρίσκουμε ότι  , από την ομοιότητα των τριγώνων
, από την ομοιότητα των τριγώνων 
 και ακόμα έχουμε
και ακόμα έχουμε  Τελικά παίρνουμε:
Τελικά παίρνουμε: και
και  (πρώτο σχήμα) ή
(πρώτο σχήμα) ή  (δεύτερο σχήμα)
(δεύτερο σχήμα)Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 11 επισκέπτες