Μια ιδιότητα του βαρυκέντρου

KARKAR · #1

: Μια ιδιότητα του βαρυκέντρου.png (18.25 KiB) Προβλήθηκε 833 φορές

Δεν είναι μια άγνωστη σχέση , αλλά είναι εντυπωσιακή , γι ' αυτό όχι παραπομπές

Αν

το βαρύκεντρο τριγώνου $\displaystyle ABC$ και οι AG,BG,CG

, τέμνουν τον περίκυκλο

του τριγώνου στα A',B',C'

αντίστοιχα , δείξτε ότι : $\dfrac{AG}{GA'}+\dfrac{BG}{GB'}+\dfrac{CG}{GG'}=3$

#2

KARKAR έγραψε:Μια ιδιότητα του βαρυκέντρου.pngΔεν είναι μια άγνωστη σχέση , αλλά είναι εντυπωσιακή , γι ' αυτό όχι παραπομπές

Αν το βαρύκεντρο τριγώνου $\displaystyle ABC$ και οι , τέμνουν τον περίκυκλο

του τριγώνου στα αντίστοιχα , δείξτε ότι : $\dfrac{AG}{GA'}+\dfrac{BG}{GB'}+\dfrac{CG}{GG'}=3$

Αν

το μέσο του

και θέσουμε MA' = x

δεν είναι δύσκολο να βρούμε :

$x = \dfrac{{{a^2}}}{{4{m_a}}}\,\,\,\kappa \alpha \iota \,\,GA' = x + \dfrac{1}{3}{m_a} = \dfrac{{4m_a^2 + 3{a^2}}}{{12{m_a}}}$ . Με τη βοήθεια του πρώτου θεωρήματος

διαμέσων προκύπτει : $\boxed{\dfrac{{GA}}{{GA'}} = \frac{{2{b^2} + 2{c^2} - {a^2}}}{{{a^2} + {b^2} + {c^2}}}}$ .

: Μια ιδιότητα του βαρυκέντρου.png (19.52 KiB) Προβλήθηκε 777 φορές

Με κυκλική εναλλαγή των γραμμάτων και πρόσθεση κατά μέλη τα ομώνυμα

κλάσματα που προκύπτουν έχουμε το ζητούμενο

Φιλικά, Νίκος

STOPJOHN · #3

KARKAR έγραψε:Μια ιδιότητα του βαρυκέντρου.pngΔεν είναι μια άγνωστη σχέση , αλλά είναι εντυπωσιακή , γι ' αυτό όχι παραπομπές

Αν το βαρύκεντρο τριγώνου $\displaystyle ABC$ και οι , τέμνουν τον περίκυκλο

του τριγώνου στα αντίστοιχα , δείξτε ότι : $\dfrac{AG}{GA'}+\dfrac{BG}{GB'}+\dfrac{CG}{GG'}=3$

$AM.AM'=\dfrac{a^{2}}{4}\Leftrightarrow MA'=\dfrac{a^{2}}{4\mu _{a}},(1), \dfrac{AG}{GA'}=\dfrac{\frac{2}{3}AM}{GM+MA'},(2), (1),(2)\Rightarrow \dfrac{AG}{GA'}=\dfrac{2b^{2}+2c^{2}-a^{2}}{3(a^{2}+b^{2}+c^{2})},(*), \dfrac{AG}{GA'}+\dfrac{BG}{GB'}+\dfrac{CG}{GG'}=\dfrac{(2b^{2}+2c^{2}-a^{2}+2a^{2}+2c^{2}-b^{2}+2a^{2}+2b^{2}-c^{2})}{3(a^{2}+b^{2}+c^{2})}=3$

Γιάννης

harrisp · #4

Ας μου επιτρέπει να θέσω και το εξής ερώτημα (ελπίζω να μην ειναι πολυ απλό):

Να δείξετε οτι ισχύει η σχεση:

$A'G\cdot B'G\cdot C'G\geq AG\cdot BG\cdot CG$

#5

KARKAR έγραψε:Δεν είναι μια άγνωστη σχέση , αλλά είναι εντυπωσιακή , γι ' αυτό όχι παραπομπές

Αν το βαρύκεντρο τριγώνου $\displaystyle ABC$ και οι , τέμνουν τον περίκυκλο

του τριγώνου στα αντίστοιχα , δείξτε ότι : $\dfrac{AG}{GA'}+\dfrac{BG}{GB'}+\dfrac{CG}{GG'}=3$

Θανάση καλησπέρα από Γρεβενά και Χρόνια Πολλά!

Εργαζόμαστε στο ακόλουθο σχήμα:

: ,Μια ιδιότητα του Βαρυκέντρου 1.png (31.28 KiB) Προβλήθηκε 766 φορές

Είναι:

$\displaystyle{\frac{AG}{GA'}=\frac{AG^2}{AG\cdot AG'} \ \ (1)}$

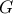Από τη δύναμη του σημείου $\displaystyle{G}$ ως προς τον περιγεγραμμένο κύκλο του τριγώνου $\displaystyle{ABC}$
είναι:

$\displaystyle{AG \cdot AG'=R^2-GO^2, \ \ (2)}$

Επίσης από το θεώρημα του Stewart στο τρίγωνο $\displaystyle{AMO}$ προκύπτει:

$\displaystyle{R^2-OG^2=\frac{a^2+b^2+c^2}{9} \ \ (3)}$

όπου $\displaystyle{a,b,c,R}$ είναι οι πλευρές του τριγώνου και η ακτίνα του περιγεγραμμένου κύκλου.

Από τις σχέσεις (1), (2) και (3) μετά από πράξεις προκύπτει:

$\displaystyle{\frac{AG}{GA'}=\frac{4m_a^2}{a^2+b^2+c^2} \ \ (4)}$

όπου $\displaystyle{m_a}$ η διάμεσος $\displaystyle{AM}$ .

Όμοια προκύπτει:

$\displaystyle{\frac{BG}{GB'}=\frac{4m_b^2}{a^2+b^2+c^2}, \ \ (5) \ \ \frac{CG}{GC'}=\frac{4m_c^2}{a^2+b^2+c^2} \ \ (6)}$

Προσθέτοντας τις (4), (5) και (6) κατά μέλη και μετά από πράξεις καταλήγουμε στη ζητούμενη.

Κώστας Δόρτσιος

.

STOPJOHN · #6

ΧΑΡΗΣ ΤΙΟΥΡΙΝΓΚ έγραψε:Ας μου επιτρέπει να θέσω και το εξής ερώτημα (ελπίζω να μην ειναι πολυ απλό):

Να δείξετε οτι ισχύει η σχεση:

$A'G\cdot B'G\cdot C'G\geq AG\cdot BG\cdot CG$

Θέτω $x=\dfrac{AG}{A'G}$
Eχει,ηδη ,αποδειχθεί ότι $x=\dfrac{2b^{2}+2c^{2}-a^{2}}{3(a^{2}+b^{2}+c^{2})}$
Eίναι $x< 1\Leftrightarrow b^{2}+c^{2}+4a^{2}\geq 0,$
Ακόμη
$x\geq 0\Leftrightarrow 2(b^{2}+c^{2})\geq a^{2}\Leftrightarrow b^{2}+c^{2}+2bccosA\geq 0,\Delta =4c^{2}(cos^{2}A-1)\leq 0,\Delta =0\Leftrightarrow A=90^{0}$

Κυκλικά και για τα άλλα κλάσματα και με πολλαπλασιασμό καταλήγουμε στην δοθείσα ανισότητα

Γιάννης

Μια ιδιότητα του βαρυκέντρου

Μια ιδιότητα του βαρυκέντρου

Re: Μια ιδιότητα του βαρυκέντρου

Re: Μια ιδιότητα του βαρυκέντρου

Re: Μια ιδιότητα του βαρυκέντρου

Re: Μια ιδιότητα του βαρυκέντρου

Re: Μια ιδιότητα του βαρυκέντρου

Μέλη σε σύνδεση