 , να γράψετε τρεις ίσους κύκλους
, να γράψετε τρεις ίσους κύκλους  , ακτίνας
, ακτίνας  ,
, έτσι ώστε να εφάπτονται στην υποτείνουσα
 , o
, o  να εφάπτεται εξωτερικά με τους άλλους δύο και επιπλέον οι
να εφάπτεται εξωτερικά με τους άλλους δύο και επιπλέον οι κύκλοι
 να εφάπτονται στις κάθετες πλευρές
να εφάπτονται στις κάθετες πλευρές  αντίστοιχα, όπως φαίνεται στο σχήμα.
αντίστοιχα, όπως φαίνεται στο σχήμα.Β) Να υπολογίσετε την περίμετρο του τριγώνου και το εμβαδόν της πράσινης επιφάνειας συναρτήσει της ακτίνας

Οποιαδήποτε ομοιότητα με την επιλογή των χρωμάτων και το πλήθος των κύκλων είναι συμπτωματική και
ουδεμία σχέση έχει με την επικαιρότητα

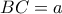 που τέμνει την
που τέμνει την  στο σημείο
στο σημείο  .
.  το μέσο της
το μέσο της  θεωρούμε σημείο
θεωρούμε σημείο  για το οποίο
για το οποίο  το τμήμα
το τμήμα  .
. με
με  και
και  με
με 
 .
. είναι ομοιόθετοι του εγγεγραμμένου
είναι ομοιόθετοι του εγγεγραμμένου  .
. , προκύπτουν οι σχέσεις:
, προκύπτουν οι σχέσεις: 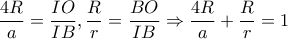
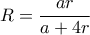 , όπου
, όπου  είναι η υποτείνουσα και
είναι η υποτείνουσα και  με
με  να συμβολίζουμε την ημιπερίμετρο του
να συμβολίζουμε την ημιπερίμετρο του  . Τα υπόλοιπα είναι απλές πράξεις καθώς όλα εκφράζονται συναρτήσει του
. Τα υπόλοιπα είναι απλές πράξεις καθώς όλα εκφράζονται συναρτήσει του