 , διαμέτρου
, διαμέτρου  και μία χορδή του
και μία χορδή του  τέτοια ώστε, αν οι
τέτοια ώστε, αν οι  τέμνονται στο σημείο
τέμνονται στο σημείο  , η
, η  να διέρχεται από το μέσο
να διέρχεται από το μέσο  της
της  . Αν η κάθετη στην
. Αν η κάθετη στην  στο σημείο
στο σημείο  τέμνει το ημικύκλιο στα σημεία
τέμνει το ημικύκλιο στα σημεία  και
και  , να αποδείξετε ότι το τρίγωνο
, να αποδείξετε ότι το τρίγωνο  είναι ισόπλευρο.
είναι ισόπλευρο.Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
 , διαμέτρου
, διαμέτρου  και μία χορδή του
και μία χορδή του  τέτοια ώστε, αν οι
τέτοια ώστε, αν οι  τέμνονται στο σημείο
τέμνονται στο σημείο  , η
, η  να διέρχεται από το μέσο
να διέρχεται από το μέσο  της
της  . Αν η κάθετη στην
. Αν η κάθετη στην  στο σημείο
στο σημείο  τέμνει το ημικύκλιο στα σημεία
τέμνει το ημικύκλιο στα σημεία  και
και  , να αποδείξετε ότι το τρίγωνο
, να αποδείξετε ότι το τρίγωνο  είναι ισόπλευρο.
είναι ισόπλευρο.Γιώργο καλησπέρα!. Το 24ωρο πέρασεgeorge visvikis έγραψε: Δίνεται ημικύκλιο κέντρου, διαμέτρου
και μία χορδή του
τέτοια ώστε, αν οι
τέμνονται στο σημείο
, η
να διέρχεται από το μέσο
της
. Αν η κάθετη στην
στο σημείο
τέμνει το ημικύκλιο στα σημεία
και
, να αποδείξετε ότι το τρίγωνο
είναι ισόπλευρο.
 τα σημεία τομής της εκ του
τα σημεία τομής της εκ του  παραλλήλου προς την
παραλλήλου προς την  με τις
με τις  αντίστοιχα. Τότε με
αντίστοιχα. Τότε με  το μέσο της
το μέσο της  και
και  θα είναι και
θα είναι και  μέσα των
μέσα των  αντίστοιχα και με
αντίστοιχα και με  τα ίχνη (λόγω του ημικυκλίου
τα ίχνη (λόγω του ημικυκλίου  ) των υψών
) των υψών  αντίστοιχα του τριγώνου
αντίστοιχα του τριγώνου  προκύπτει ότι
προκύπτει ότι είναι σημεία του κύκλου Euler
είναι σημεία του κύκλου Euler  του τριγώνου
του τριγώνου  .
.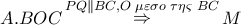 το μέσο της
το μέσο της  παραλληλόγραμμο
παραλληλόγραμμο 


 εγγράψιμο
εγγράψιμο
 ισόπλευρο και το ζητούμενο έχει αποδειχθεί
ισόπλευρο και το ζητούμενο έχει αποδειχθεί , συναρτήσει της ακτίνας
, συναρτήσει της ακτίνας  του ημικυκλίου.
του ημικυκλίου.Από το 1ο Θεώρημα των διαμέσων στο τρίγωνοgeorge visvikis έγραψε: ...Να υπολογιστεί το άθροισμα, συναρτήσει της ακτίνας
του ημικυκλίου.
 έχουμε:
έχουμε: 

 με τα
με τα  ως τυχόντα σημεία επί των πλευρών του
ως τυχόντα σημεία επί των πλευρών του  αντιστοίχως, σύμφωνα με το παρακάτω Λήμμα 1,
αντιστοίχως, σύμφωνα με το παρακάτω Λήμμα 1,  λόγω
λόγω  .
Με τα
.
Με τα  ως τα σημεία τομής των
ως τα σημεία τομής των  αντιστοίχως, από το ημικύκλιο με διάμετρο
αντιστοίχως, από το ημικύκλιο με διάμετρο  σύμφωνα με το παρακάτω Λήμμα 2,
σύμφωνα με το παρακάτω Λήμμα 2, 
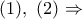


 και
και 

 συμπεραίνεται ότι το ισοσκελές τρίγωνο
συμπεραίνεται ότι το ισοσκελές τρίγωνο  είναι ισόπλευρο και το ζητούμενο έχει αποδειχθεί.
είναι ισόπλευρο και το ζητούμενο έχει αποδειχθεί. και έστω
και έστω 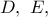 τυχόνυα σημεία επί των πλευρών του
τυχόνυα σημεία επί των πλευρών του  αντιστοίχως. Αποδείξτε ότι
αντιστοίχως. Αποδείξτε ότι  , όπου
, όπου  είναι το μέσον του
είναι το μέσον του  και
και 
 και έστω
και έστω 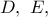 τα σημεία τομής των πλευρών του
τα σημεία τομής των πλευρών του  αντιστοίχως, από το ημικύκλιο με διάμετρο
αντιστοίχως, από το ημικύκλιο με διάμετρο  και έστω το σημείο
και έστω το σημείο  όπου
όπου  είναι το μέσον του
είναι το μέσον του  Αποδείξτε ότι
Αποδείξτε ότι 
vittasko έγραψε:ΛΗΜΜΑ 1. - Δίνεται τρίγωνοκαι έστω
τυχόνυα σημεία επί των πλευρών του
αντιστοίχως. Αποδείξτε ότι
, όπου
είναι το μέσον του
και
 Δια των σημείων
Δια των σημείων  φέρνουμε τις παράλληλες ευθείες προς την
φέρνουμε τις παράλληλες ευθείες προς την  οι οποίες τέμνουν την ευθεία
οι οποίες τέμνουν την ευθεία  στα σημεία
στα σημεία  αντιστοίχως.
αντιστοίχως.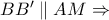



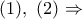

 ισχύει
ισχύει 

 και το Λήμμα 1 έχει αποδειχθεί.
και το Λήμμα 1 έχει αποδειχθεί. περνάει από το βαρύκεντρο του δοσμένου τριγώνου.
περνάει από το βαρύκεντρο του δοσμένου τριγώνου.Έστω το σημείοvittasko έγραψε:ΛΗΜΜΑ 2. - Δίνεται τρίγωνοκαι έστω
τα σημεία τομής των πλευρών του
αντιστοίχως, από το ημικύκλιο με διάμετρο
και έστω το σημείο
όπου
είναι το μέσον του
Αποδείξτε ότι
 ως το ορθόκεντρο του δοσμένου τριγώνου
ως το ορθόκεντρο του δοσμένου τριγώνου  και έστω το σημείο
και έστω το σημείο  και προφανώς ισχύει
και προφανώς ισχύει 
 Από τα όμοια ορθογώνια τρίγωνα
Από τα όμοια ορθογώνια τρίγωνα  έχουμε
έχουμε 

 έχουμε
έχουμε 

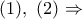

 Ομοίως, από τα όμοια ορθογώνια τρίγωνα
Ομοίως, από τα όμοια ορθογώνια τρίγωνα 



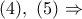



 έχουμε
έχουμε  και
και 

 λόγω
λόγω 
 και
και 
 και το Λήμμα 2 έχει αποδειχθεί.
και το Λήμμα 2 έχει αποδειχθεί. όπου
όπου και
και  οι πλευρές του δοσμένου τριγώνου
οι πλευρές του δοσμένου τριγώνου 
Ας δείξουμε μια ελαφρά γενίκευση του λήμματος αυτού.
 ώστε να ισχύει
ώστε να ισχύει  . Τα
. Τα  και
και  και η
και η  τέμνει την
τέμνει την  στο
στο 

 όπως στο σχήμα:
όπως στο σχήμα: και
και  Με πρόσθεση παίρνουμε
Με πρόσθεση παίρνουμε  .
.  έχουμε το ως άνω Λήμμα 1. Φιλικά, Γιώργος.
έχουμε το ως άνω Λήμμα 1. Φιλικά, Γιώργος.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες