Ισοσκελές Τραπέζιο Και εγγράψιμο τετράπλευρο

chris · #1

Ένα όμορφο θέμα απο mathlinks

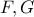Έστω ενα ισοσκελές τραπέζιο εγγεγραμμένο σε κύκλο με $AD \parallel BC$ .Έστω το μέσο του τόξου $\widehat{BC}$ και ένα τυχαίο σημείο του τμήματος .Μια ευθεία που διέρχεται απο το είναι παράλληλη στην και τέμνει τα τμήματα και στα σημεία αντίστοιχα.Αν η τέμνει τον κύκλο στο σημείο να αποδειχθεί οτι το τετράπλευρο είναι εγγράψιμο.

: Isoskeles trapezio.png (30.7 KiB) Προβλήθηκε 902 φορές

#2

Περίεργο πρόβλημα και δέκα μέρες τώρα αναπάντητο.

Ας δούμε μία λύση που ταιριάζει στην Β' Λυκείου του περασμένου αιώνα ( εκεί στα μέσα της δεκαετίας του 60...

) και συμπαθάτε με, που δεν μπόρεσα να βρω κάτι απλούστερο.

$\bullet$ Έστω τα σημεία $K\equiv (O)\cap MF$ και $L\equiv (O)\cap HG,$ όπου (O)

είναι ο περίκυκλος του δοσμένου τραπεζίου ABCD

και σύμφωνα με το παρακάτω Λήμμα, ισχύει $KL\parallel AD.$

Έστω το σημείο $Z\equiv BC\cap MF$ και έχουμε $\angle MFG = \angle BZF = \angle BMK + \angle MBC$ ,(1)

Επίσης έχουμε $\angle MHG\equiv MHL = \angle MBK = \angle KBC + \angle MBC$ ,(2)

Από $(1),\ (2)$ $\Longrightarrow$ $\angle MFG + \angle MHG = \angle BMK + \angle KBC + 2\angle MBC =$ $\angle BCK + \angle KBC + \angle BKC = 180^{o}$ ,(3)

Από

συμπεραίνεται ότι το τετράπλευρο FMHG

είναι εγγράψιμο και το ζητούμενο έχει αποδειχθεί.

: Ισοσκελές τραπέζιο και εγγράψιμο τετράπλευρο.; f=22_t=13010.PNG (30.21 KiB) Προβλήθηκε 759 φορές

ΛΗΜΜΑ. - Δίνεται τραπέζιο $\triangle ABCD$ με $BC\parallel AD,$ εγγεγραμμένο σε κύκλο και έστω τυχόν σημείο επί της διχοτόμου της γωνίας $\angle BDC.$ Δια του φέρνουμε την παράλληλη ευθεία προς την η οποία τέμνει τις $BD,\ CD,$ στα σημεία $F,\ G$ αντιστοίχως και έστω $H,\ M,\ K,\ L,$ τα σημεία τομής του κύκλου από τις ευθείες $AE,\ DE,\ MF,\ HG,$ αντιστοίχως. Αποδείξτε ότι $KL\parallel AD.$

Κώστας Βήττας.

ΥΓ.1 - Θα βάλω αγότερα την απόδειξη που έχω υπόψη μου για το παραπάνω Λήμμα, με χρήση του Θεωρήματος Pascal.

ΥΓ.2 - Τελικά η απόδειξη του Λήμματος βγαίνει και με στοιχειώδη μέσα ( χωρίς το Θεώρημα Pascal ). Αποδεικνύεται εύκολα ότι τα σημεία $C,\ E,\ K$ είναι συνευθειακά και ότι το τετράπλευρο CEGH,

είναι επίσης εγγράψιμο και προκύπτει άμεσα ότι $KL\parallel AD.$

Η τελική λύση λοιπόν είναι είναι συμβατή με την τωρινή Β' Λυκείου ( δεν χρειάζεται να πάμε Χαλκίδα, μέσω Αράχωβας ... ).

chris · #3

Κώστα ευχαριστώ!Ίσως υπερεκτίμησα τις δυνάμεις της Β Λυκείου

Έστω

το σημείο τομής του κύκλου και της

και $\displaystyle \left\{F{'} \right\}\equiv MJ \cap DB.$
Εφόσον $\displaystyle \angle{CJM}=\angle{BDM}$ έχουμε:
$\displaystyle \left(DJF{'}E$ εγγράψιμο $\displaystyle )\Longrightarrow \left(\angle{DF{'}E}=\angle{DJC}=\angle{DBC} \right)\Longrightarrow EF{'}\parallel BC\Longrightarrow F\equiv F{'}$

Όμως:
$\displaystyle \angle{ADC}+\angle{ABC}=180^{o}\Longrightarrow \angle{AHC}+\angle{DCB}=180^{o}\Longrightarrow \angle{AHC}+\angle{DGF}=180^{o}\Longrightarrow \angle{AHC}=\angle{EGC}$

άρα το τετράπλευρο EGCH

είναι εγγράψιμο και τελικα:
$\angle {FGH}=\angle {JCH}=\angle {FMH} \pmod\pi \Longrightarrow FMHG$ εγγράψιμο

: Isoskeles trapezio.png (37.38 KiB) Προβλήθηκε 726 φορές

halgeo · #4

Με ΑD=AB=DC που τα έχετε αυτά τα τραπέζια . Τέτοια τραπέζια σχεδιάζω άπειρα . Εσείς δεν έχετε ούτε ένα .

halgeo · #5

ΘΕΜΑ: Ισοσκελές τραπέζιο εγγεγραμμένο σε κύκλο και το οποίο έχει την μικρή βάση ίση με τις δύο μη παράλληλες πλευρές του.

Στον κύκλο με ακτίνα ρ=145 βρίσκω και δύο σημεία του Η(-87,-116) και Κ(87,-116) με ΗΚ//ΑΒ (ΑΒ οριζόντια διάμετρο ) Να βρείτε και δύο άλλα σημεία του κύκλου Ε και Ζ με ΕΖ//ΑΒ //ΗΚ . Να βρείτε τις συντεταγμένες των Ε και Ζ και να αποδείξετε ότι ισχύει ΕΗ=ΗΚ=ΚΖ . Τέτοια τραπέζια που έχουν την μικρή βάση ίση με τις δύο μη παράλληλες πλευρές σχεδιάζω άπειρα με διαβήτη και χάρακα . ΕΖ είναι η μεγάλη βάση και ΗΚ είναι η μικρή βάση . Επαληθεύστε και το θεώρημα του Πτολεμαίου ΕΚ . ΖΗ = ΕΖ . ΗΚ + ΕΗ . ΖΚ .

cool geometry · #6

Αυτή τη λύση είχα κι εγώ κατά νου. Εύκολα $KL\left | \right |AD$

$\angle MFG=\angle BZF(BC\left | \right |FG)=\angle MBC+\angle BMK(1)$
$\angle MHG=\angle MBK=\angle MBC+\angle KBC(2)$
$(1),(2)\Rightarrow \angle MHG+\angle MFG=2\angle MBC+\angle BMK+\angle KBC=180^{0}-\angle BMC+\angle BCK+\angle KBC=\angle BKC+\angle BCK+\angle KBC=180^{0}.$

Henri van Aubel · #7

Βάζω μία λύση με στοιχειώδη μέσα, απορώ πως δεν την έβαλε κάποιος άλλος...

Έχουμε $\angle EGC\equiv \angle FGC^{FG\parallel AD}=\angle ADC=\angle AHC\equiv \angle EHC,$

άρα το τετράπλευρο EGHC

είναι εγγράψιμο κι έτσι $\angle FGH\equiv \angle EGH=\pi -\angle ECH\left ( 1 \right )$

Έστω $K\equiv DM\cap BC,$ τότε έχουμε $\displaystyle \frac{ED}{FD}^{FE\parallel BK}=\frac{DK}{DB}^{\vartriangle BDK\sim \vartriangle DMC}=\frac{DC}{DM}\left ( 2 \right )$

Επιπλέον $\angle FDM=\angle EDC\left ( 3 \right )$

Από $\left ( 2 \right ),\left ( 3 \right )\Rightarrow \vartriangle FDM\sim \vartriangle EDC\Rightarrow \angle FMD=\angle ECD\left ( 4 \right )$

Ακόμα $\angle DMH=\angle DCH$ ως εγγεγραμμένες γωνίες που βαίνουν στο ίδιο τόξο , επομένως και σύμφωνα με την $\left ( 4 \right )$ θα έχουμε $\angle FMH=\angle ECH\left ( 5 \right )$

Από $\left ( 1 \right ),\left ( 5 \right )\Rightarrow \angle FMH+\angle FGH=\pi$ και άρα F,G,H,M

ομοκυκλικά, όπως θέλαμε.

Υ.Σ Υπέροχο πρόβλημα για Β Λυκείου, αλλά για ελάχιστα παιδιά!

Έπεσα πάνω στο θέμα αυτό κατά την περιήγησή μου στον φάκελο της β Λυκείου

Ισοσκελές Τραπέζιο Και εγγράψιμο τετράπλευρο

Ισοσκελές Τραπέζιο Και εγγράψιμο τετράπλευρο

Re: Ισοσκελές Τραπέζιο Και εγγράψιμο τετράπλευρο

Re: Ισοσκελές Τραπέζιο Και εγγράψιμο τετράπλευρο

Re: Ισοσκελές Τραπέζιο Και εγγράψιμο τετράπλευρο

Re: Ισοσκελές Τραπέζιο Και εγγράψιμο τετράπλευρο

Re: Ισοσκελές Τραπέζιο Και εγγράψιμο τετράπλευρο

Re: Ισοσκελές Τραπέζιο Και εγγράψιμο τετράπλευρο

Μέλη σε σύνδεση