1. Να δειχθεί οτι το άθροισμα
 είναι σταθερό.
είναι σταθερό.2. Να βρεθεί η θέση της ε για την οποία το (ΟΑΒ) γίνεται ελάχιστο.
Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
 είναι σταθερό.
είναι σταθερό. πρέπει να είναι κυρτή, για να σχηματίζονται τα τρίγωνα.
πρέπει να είναι κυρτή, για να σχηματίζονται τα τρίγωνα. .
.  αντίστοιχα.
αντίστοιχα. 
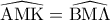 ως κατακορυφήν, έχουμε:
ως κατακορυφήν, έχουμε: 
 , που είναι σταθερό.
, που είναι σταθερό. .
. 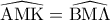 ως κατακορυφήν, έχουμε:
ως κατακορυφήν, έχουμε: 
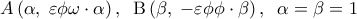 .
.  , σταθερό.
, σταθερό.


![\left( {a^2 + b^2} \right)\left( {c^2 + d^2} \right) \geqslant \left( {ac + bd} \right)^{^2 } \Rightarrow \left[ {\left( {a^2 + b^2} \right)\left( {c^2 + d^2} \right)} \right]_{\min } = \left( {ac + bd} \right)^{^2 } ,\alpha \nu \;ac + bd\;\sigma \tau \alpha \theta \varepsilon \rho \eta . \left( {a^2 + b^2} \right)\left( {c^2 + d^2} \right) \geqslant \left( {ac + bd} \right)^{^2 } \Rightarrow \left[ {\left( {a^2 + b^2} \right)\left( {c^2 + d^2} \right)} \right]_{\min } = \left( {ac + bd} \right)^{^2 } ,\alpha \nu \;ac + bd\;\sigma \tau \alpha \theta \varepsilon \rho \eta .](/forum/ext/geomar/texintegr/latexrender/pictures/ddb35c17f5e7d4fe34abda88326eba44.png)
 σταθερό, τότε το γινόμενό τους έχει μέγιστο γινόμενο όταν είναι ίσοι, αν μπορεί να γίνουν ίσοι.
σταθερό, τότε το γινόμενό τους έχει μέγιστο γινόμενο όταν είναι ίσοι, αν μπορεί να γίνουν ίσοι.  , δηλαδή όταν
, δηλαδή όταν  μέσο
μέσο  .
.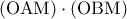 γίνεται ελάχιστο, άρα το
γίνεται ελάχιστο, άρα το  γίνεται ελάχιστο, οπότε και το
γίνεται ελάχιστο, οπότε και το  γίνεται ελάχιστο.
γίνεται ελάχιστο.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες