 , για τα οποία από τις ανισώσεις
, για τα οποία από τις ανισώσεις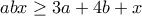 ,
,  ,
, 
συνεπάγεται η ανίσωση
 .
.Συντονιστής: exdx
 , για τα οποία από τις ανισώσεις
, για τα οποία από τις ανισώσεις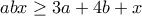 ,
,  ,
, 
 .
.
 , η ανισότητα
, η ανισότητα 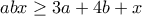 γίνεται
γίνεται  που ισχύει για
που ισχύει για  , που δεν οδηγεί στην ανισότητα
, που δεν οδηγεί στην ανισότητα  , οπότε πρέπει
, οπότε πρέπει 
 , για να ισχύει η ανισότητα
, για να ισχύει η ανισότητα  αρκεί
αρκεί  (1).
(1).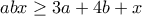 , για να ισχύει η (1) αρκεί
, για να ισχύει η (1) αρκεί  , με
, με  .
. , οπότε αν οι μη αρνητικές μεταβλητές
, οπότε αν οι μη αρνητικές μεταβλητές  πάρουν το ελάχιστο γινόμενό τους
πάρουν το ελάχιστο γινόμενό τους  , αφού αυτό είναι σταθερό, το άθροισμά τους θα έχει ελάχιστη τιμή, όταν γίνουν ίσοι, δηλαδή όταν
, αφού αυτό είναι σταθερό, το άθροισμά τους θα έχει ελάχιστη τιμή, όταν γίνουν ίσοι, δηλαδή όταν 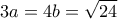 , άρα
, άρα  .
. .
.Όντως ανΓιώργος Ρίζος έγραψε: ↑Πέμ Ιούλ 07, 2022 7:50 pmΓια θετικά, για να ισχύει η ανισότητα
αρκεί
(1).
Αφού ισχύει, για να ισχύει η (1) αρκεί
, με
.
 τότε
τότε  , αλλά γιατί
, αλλά γιατί 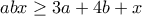 και
και  είναι ισοδύναμες (υπό τους υπόλοιπους περιορισμούς
είναι ισοδύναμες (υπό τους υπόλοιπους περιορισμούς  και
και 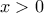 );
); , η ανισότητα
, η ανισότητα 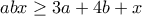 (1) γίνεται
(1) γίνεται  που ισχύει για
που ισχύει για  και δεν οδηγεί στην ανισότητα
και δεν οδηγεί στην ανισότητα  , οπότε πρέπει
, οπότε πρέπει  .
. για κάθε
για κάθε 
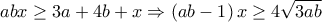 (2), με το «ίσον» όταν
(2), με το «ίσον» όταν  .
. η ανισότητα (1) είναι αδύνατη.
η ανισότητα (1) είναι αδύνατη. , κι έτσι η ανισότητα (2) η ανισότητα γράφεται
, κι έτσι η ανισότητα (2) η ανισότητα γράφεται  .
.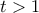 η συνάρτηση
η συνάρτηση  είναι γνησίως φθίνουσα, άρα
είναι γνησίως φθίνουσα, άρα 
 από την (1) αρκεί το
από την (1) αρκεί το  να πάρει μέγιστη τιμή
να πάρει μέγιστη τιμή 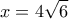 .
.Καλησπέρα Γιώργο,Γιώργος Ρίζος έγραψε: ↑Δευ Ιούλ 11, 2022 3:26 pmΑλέξανδρε, κατ' αρχάς σε ευχαριστώ για τον κόπο να ασχοληθείς με την απάντησή μου και για τη διόρθωση που έκανες. Επίσης ευχαριστώ για το ευγενικό "κ. Γιώργο", αλλά προτιμώ την οικειότητα και την ευγένεια της απλής ονομαστικής προσφώνησης. Εξάλλου, στοαισθάνομαι μαθητευόμενος, όπως άλλωστε οι περισσότεροι από εμάς, πιστεύω.
Κάνω μια 2η προσπάθεια. Θα χαρώ να δω ξανά τις παρατηρήσεις σας σε τυχόν λάθη ή ελλείψεις στην απάντηση:
Αν, η ανισότητα
(1) γίνεται
που ισχύει για
και δεν οδηγεί στην ανισότητα
, οπότε πρέπει
.
Είναιγια κάθε

Οπότε(2), με το «ίσον» όταν
.
Ανη ανισότητα (1) είναι αδύνατη.
Πρέπει, λοιπόν,, κι έτσι η ανισότητα (2) η ανισότητα γράφεται
.
Εύκολα βρίσκουμε ότι γιαη συνάρτηση
είναι γνησίως φθίνουσα, άρα
Για να προκύψει, λοιπόν η ανισότητααπό την (1) αρκεί το
να πάρει μέγιστη τιμή
.
 θα βρεθούν
θα βρεθούν  ώστε
ώστε  ( όταν ισχύουν οι αρχικές συνθήκες της εκφώνησης).
( όταν ισχύουν οι αρχικές συνθήκες της εκφώνησης). , αλλά αυτή είναι μια πιο ασθενής εκδοχή της αρχικής (1)
, αλλά αυτή είναι μια πιο ασθενής εκδοχή της αρχικής (1) 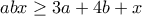 . Μας λείπει το "
. Μας λείπει το " ", για να έχουμε
", για να έχουμε  , δεδομένων πάντα των περιορισμών για τα
, δεδομένων πάντα των περιορισμών για τα  .
.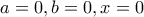 οδηγεί σε άτοπο.
οδηγεί σε άτοπο.  γράφεται
γράφεται  και άμεσα πρέπει
και άμεσα πρέπει  , οπότε παίρνουμε
, οπότε παίρνουμε  και τώρα (πράξεις)
και τώρα (πράξεις)
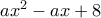 έχει δύο ρίζες, τότε αυτές είναι θετικές. Για κάθε τιμή του α κείμενη εντός του διαστήματός τους, και για την τιμή του
έχει δύο ρίζες, τότε αυτές είναι θετικές. Για κάθε τιμή του α κείμενη εντός του διαστήματός τους, και για την τιμή του  είναι
είναι  (πράξεις) και
(πράξεις) και  (πράξεις), δεν μας κάνει.
(πράξεις), δεν μας κάνει.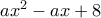 να έχει διπλή ρίζα ή να μην έχει ρίζες, που γίνεται αν και μόνον αν
να έχει διπλή ρίζα ή να μην έχει ρίζες, που γίνεται αν και μόνον αν  . Αυτές είναι και οι ζητούμενες τιμές αφού πράγματι συνεπάγονται, όπως εύκολα διαπιστώνουμε την
. Αυτές είναι και οι ζητούμενες τιμές αφού πράγματι συνεπάγονται, όπως εύκολα διαπιστώνουμε την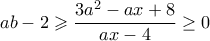
 και πάνω, να βρίσκονται ομοίως και από την υπερβολή
και πάνω, να βρίσκονται ομοίως και από την υπερβολή  και πάνω (σε σύστημα aOb). Αυτό δεν γίνεται αν στο πρώτο τεταρτημόριο οι υπερβολές έχουν κοινά σημεία (φανερό το γιατί(;)) , αλλά μόνο αν αυτές εφάπτονται εφάπτονται ή δεν έχουν κοινά σημεία, και η πρώτη είναι πάνω από την δεύτερη. Αυτά για να συμβούν πρέπει το σύστημα των δύο υπερβολών να οδηγεί σε δευτεροβάθμια εξίσωση με μη θετική διακρίνουσα. (Βρίσκουμε την
και πάνω (σε σύστημα aOb). Αυτό δεν γίνεται αν στο πρώτο τεταρτημόριο οι υπερβολές έχουν κοινά σημεία (φανερό το γιατί(;)) , αλλά μόνο αν αυτές εφάπτονται εφάπτονται ή δεν έχουν κοινά σημεία, και η πρώτη είναι πάνω από την δεύτερη. Αυτά για να συμβούν πρέπει το σύστημα των δύο υπερβολών να οδηγεί σε δευτεροβάθμια εξίσωση με μη θετική διακρίνουσα. (Βρίσκουμε την  . Στην συνέχεια έλεγχος, επαλήθευση κ.λπ.)
. Στην συνέχεια έλεγχος, επαλήθευση κ.λπ.)Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες