 η εξίσωση
η εξίσωση 
έχει ρίζα τουλάχιστον ίση με
 ;
;Συντονιστής: exdx
 η εξίσωση
η εξίσωση 
 ;
;
 και οι ισότητες ισχύουν ακριβώς όταν
και οι ισότητες ισχύουν ακριβώς όταν  . Επομένως
. Επομένως
 είναι
είναι  , έχουμε λύση
, έχουμε λύση  ακριβώς όταν
ακριβώς όταν 
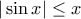 . Η ανισότητα αυτή αποδεικνύεται στο σχολικό βιβλίο της Γ' Λυκείου αλλά, χρησιμοποιεί ύλη των προηγούμενων τάξεων, οπότε αποφάσισα να την τοποθετήσω εδώ.
. Η ανισότητα αυτή αποδεικνύεται στο σχολικό βιβλίο της Γ' Λυκείου αλλά, χρησιμοποιεί ύλη των προηγούμενων τάξεων, οπότε αποφάσισα να την τοποθετήσω εδώ. είναι
είναι 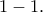 Δεν το τοποθέτησα όμως εδώ γιατί θεώρησα ότι η μέθοδος χωρίς χρήση παραγώγων που είναι άμεση, είναι για μαθητή λίγο επίπονη. Η ανάλυση που κάνουμε σε αυτές τις περιπτώσεις είναι να δούμε καταρχάς αν υπάρχει σχέση μεταξύ των τόξων που αναφέρονται στους τριγωνομετρικούς αριθμούς και του "αποτελέσματος". Εδώ για παράδειγμα βλέπουμε ότι:
Δεν το τοποθέτησα όμως εδώ γιατί θεώρησα ότι η μέθοδος χωρίς χρήση παραγώγων που είναι άμεση, είναι για μαθητή λίγο επίπονη. Η ανάλυση που κάνουμε σε αυτές τις περιπτώσεις είναι να δούμε καταρχάς αν υπάρχει σχέση μεταξύ των τόξων που αναφέρονται στους τριγωνομετρικούς αριθμούς και του "αποτελέσματος". Εδώ για παράδειγμα βλέπουμε ότι: 
 και
και  καταλήγουμε στο αποτέλεσμα
καταλήγουμε στο αποτέλεσμα 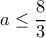 .
.Καλή Πρωτομαγιά! Καλημέρα!S.E.Louridas έγραψε: ↑Παρ Μάιος 01, 2020 11:39 amΚαλημέρα και Καλή Πρωτομαγιά.
Πολύ Όμορφη η άσκηση αλλά σίγουρα και η λύση του Κώστα. Προσωπικά έλυσα το όμορφο αυτό θέμα χρησιμοποιώντας ότι ηείναι
Δεν το τοποθέτησα όμως εδώ γιατί θεώρησα ότι η μέθοδος χωρίς χρήση παραγώγων που είναι άμεση, είναι για μαθητή λίγο επίπονη. Η ανάλυση που κάνουμε σε αυτές τις περιπτώσεις είναι να δούμε καταρχάς αν υπάρχει σχέση μεταξύ των τόξων που αναφέρονται στους τριγωνομετρικούς αριθμούς και του "αποτελέσματος". Εδώ για παράδειγμα βλέπουμε ότι:

Άρα γιακαι
καταλήγουμε στο αποτέλεσμα
.
 .
. 
 . Άρα
. Άρα  .
.Σαφέστατα αλλά δεν μίλησα για αυτό το σημείο, απλά θεώρησα ότι δεν είναι γνωστή για την Β' Λυκείου η ανισότητα:Al.Koutsouridis έγραψε: ↑Παρ Μάιος 01, 2020 12:03 pmΚαλή Πρωτομαγιά! Καλημέρα!S.E.Louridas έγραψε: ↑Παρ Μάιος 01, 2020 11:39 amΚαλημέρα και Καλή Πρωτομαγιά.
Πολύ Όμορφη η άσκηση αλλά σίγουρα και η λύση του Κώστα. Προσωπικά έλυσα το όμορφο αυτό θέμα χρησιμοποιώντας ότι ηείναι
Δεν το τοποθέτησα όμως εδώ γιατί θεώρησα ότι η μέθοδος χωρίς χρήση παραγώγων που είναι άμεση, είναι για μαθητή λίγο επίπονη. Η ανάλυση που κάνουμε σε αυτές τις περιπτώσεις είναι να δούμε καταρχάς αν υπάρχει σχέση μεταξύ των τόξων που αναφέρονται στους τριγωνομετρικούς αριθμούς και του "αποτελέσματος". Εδώ για παράδειγμα βλέπουμε ότι:

Άρα γιακαι
καταλήγουμε στο αποτέλεσμα
.
Τα παραπάνω πολύ πιθανόν να είναι και ο τρόπος κατασκευής της άσκησης. Δηλαδή η επιλογή μια συνάρτησης με χαρακτηριστικά που θέλουμε και το ντύσιμό της με άλλες δυο τρεις ιδιότητες που θέλουμε να εξετάσουμε.
Πάντως αν κάνουμε τις παραπάνω αντικαταστάσεις, πάλι μπορούμε να αποφύγουμε την μελέτη της συνάρτησης.

Από την άλλη. Άρα
.
 (δυστυχώς έχω πολύ καιρό να διδάξω στην τάξη αυτή) και θα έπρεπε πρώτα να αποδειχθεί. Εντάξει η άσκηση είναι πολύ καλή και η εδώ κουβέντα επίσης. Και πάλι καλή Πρωτομαγιά.
(δυστυχώς έχω πολύ καιρό να διδάξω στην τάξη αυτή) και θα έπρεπε πρώτα να αποδειχθεί. Εντάξει η άσκηση είναι πολύ καλή και η εδώ κουβέντα επίσης. Και πάλι καλή Πρωτομαγιά.Επ!! Σωτήρη, χρόνια Πολλά!!Al.Koutsouridis έγραψε: ↑Παρ Μάιος 01, 2020 12:03 pmΚαλή Πρωτομαγιά! Καλημέρα!S.E.Louridas έγραψε: ↑Παρ Μάιος 01, 2020 11:39 amΚαλημέρα και Καλή Πρωτομαγιά.
Πολύ Όμορφη η άσκηση αλλά σίγουρα και η λύση του Κώστα. Προσωπικά έλυσα το όμορφο αυτό θέμα χρησιμοποιώντας ότι ηείναι
Δεν το τοποθέτησα όμως εδώ γιατί θεώρησα ότι η μέθοδος χωρίς χρήση παραγώγων που είναι άμεση, είναι για μαθητή λίγο επίπονη. Η ανάλυση που κάνουμε σε αυτές τις περιπτώσεις είναι να δούμε καταρχάς αν υπάρχει σχέση μεταξύ των τόξων που αναφέρονται στους τριγωνομετρικούς αριθμούς και του "αποτελέσματος". Εδώ για παράδειγμα βλέπουμε ότι:

Άρα γιακαι
καταλήγουμε στο αποτέλεσμα
.
Τα παραπάνω πολύ πιθανόν να είναι και ο τρόπος κατασκευής της άσκησης. Δηλαδή η επιλογή μια συνάρτησης με χαρακτηριστικά που θέλουμε και το ντύσιμό της με άλλες δυο τρεις ιδιότητες που θέλουμε να εξετάσουμε.
Πάντως αν κάνουμε τις παραπάνω αντικαταστάσεις, πάλι μπορούμε να αποφύγουμε την μελέτη της συνάρτησης.

Από την άλλη. Άρα
.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες