
α)Να βρεθεί το πεδίο ορισμού.
β)Να εξετάσετε αν η συνάρτηση είναι άρτια η περιττή.
γ)Αν Μ(-1,-10) ανήκει στη γραφική παράσταση της f.
i)Να βρεθεί το α
ii)Να απλοποιήσετε την f
iii)Να μελετήσετε την f ως προς τη μονοτονία.
Απαντώ σύντομα στα εύκολα
α)

β)
 περιττή.
περιττή.γ)i)

γ)ii)
 για
για 
γ)iii) Εδώ το βιβλίο γράφει (χωρίς να υπάρχει λύση) οτι η f είναι γνησίως αύξουσα. Πως προκύπτει αυτό το συμπέρασμα από τη στιγμή που η f είναι ορισμένη σε ένωση διαστημάτων? Ευχαριστώ πολύ. (Αναφέρομαι σε λύση με ύλη 2ας λυκείου προφανώς.)

 στο πεδίο ορισμού (*) με
στο πεδίο ορισμού (*) με 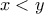 ισχύει
ισχύει  .
.  , όπου
, όπου  , η συνάρτηση
, η συνάρτηση  . Τι λες, είναι ή δεν είναι γνήσια αύξουσα; Το πεδίο ορισμού είναι διάστημα;
. Τι λες, είναι ή δεν είναι γνήσια αύξουσα; Το πεδίο ορισμού είναι διάστημα;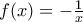 είναι γνησίως αύξουσα στα διαστήματα
είναι γνησίως αύξουσα στα διαστήματα  και
και  αλλά δεν είναι γνησίως αύξουσα στο πεδίο ορισμού της διότι τα όριά της στο σημείο που δεν ορίζεται δεν είναι πραγματικοί αριθμοί.
αλλά δεν είναι γνησίως αύξουσα στο πεδίο ορισμού της διότι τα όριά της στο σημείο που δεν ορίζεται δεν είναι πραγματικοί αριθμοί. για
για  . Η συνάρτηση με τον ίδιο τύπο αλλά ορισμένη σε όλο το
. Η συνάρτηση με τον ίδιο τύπο αλλά ορισμένη σε όλο το  είναι γνήσια αύξουσα (άμεσο), άρα πόσο μάλλον και ο περιορισμός της στο
είναι γνήσια αύξουσα (άμεσο), άρα πόσο μάλλον και ο περιορισμός της στο  . Με λίγα λόγια για την
. Με λίγα λόγια για την  είτε τα
είτε τα  .
. είναι μεν σωστό, αλλά δεν εφαρμόζεται εδώ.
είναι μεν σωστό, αλλά δεν εφαρμόζεται εδώ.
 και
και 
 και
και  είναι πραγματικοί αριθμοί οπότε
είναι πραγματικοί αριθμοί οπότε 

 ) !
) !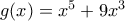 με
με  , δείχνεις ότι είναι γνησίως αύξουσα και μετά λες ό,τι θες. Απλώς, στα πλαίσια του σχολικού βιβλίου, δεν έχει νόημα μονοτονία σε ένωση ξένων διαστημάτων.
, δείχνεις ότι είναι γνησίως αύξουσα και μετά λες ό,τι θες. Απλώς, στα πλαίσια του σχολικού βιβλίου, δεν έχει νόημα μονοτονία σε ένωση ξένων διαστημάτων.
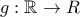 , συνεχής, η οποία, αν περιοριστεί στο
, συνεχής, η οποία, αν περιοριστεί στο  ισούται με την
ισούται με την  και
και  με
με  . Tα
. Tα  μπορεί να είναι και τα
μπορεί να είναι και τα  ,
,  αντίστοιχα.
αντίστοιχα.  , με
, με  ,
, 
 με
με  ισχύει
ισχύει 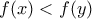 .
. 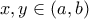 και αν
και αν  αφού η συνάρτηση είναι γνησίως αύξουσα σ' αυτά τα διαστήματα.
αφού η συνάρτηση είναι γνησίως αύξουσα σ' αυτά τα διαστήματα.  και
και  .
. . Αν όχι:
. Αν όχι:  . Έτσι,
. Έτσι,  .
.  άτοπο.
άτοπο. και συνεπώς
και συνεπώς  , τότε
, τότε  και παίρνοντας όριο με
και παίρνοντας όριο με  , βρίσκουμε ότι
, βρίσκουμε ότι  , οπότε
, οπότε 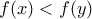 .
. .
. στο
στο  .
.