 η εξίσωση
η εξίσωση
έχει ακριβώς έξι διαφορετικές ρίζες στο διάστημα
![\left [ 2a \pi , \left ( a^2+1 \right ) \pi \right ] \left [ 2a \pi , \left ( a^2+1 \right ) \pi \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/7cc23bb9f59097a97abd6258b90ab48d.png) ;
;Υποδείξτε αυτές τις λύσεις.
Συντονιστής: exdx
 η εξίσωση
η εξίσωση
![\left [ 2a \pi , \left ( a^2+1 \right ) \pi \right ] \left [ 2a \pi , \left ( a^2+1 \right ) \pi \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/7cc23bb9f59097a97abd6258b90ab48d.png) ;
;




 Στη συγκεκριμένη μορφή όμως παρατηρούμε ότι αν
Στη συγκεκριμένη μορφή όμως παρατηρούμε ότι αν 
 μηδενίζεται. Επομένως αυτή τη λύση τη δεχόμαστε μόνο για ζυγούς αριθμούς
μηδενίζεται. Επομένως αυτή τη λύση τη δεχόμαστε μόνο για ζυγούς αριθμούς  και άρα μπορούμε να τη μετασχηματίσουμε
και άρα μπορούμε να τη μετασχηματίσουμε με
με 



![\left [ 2a \pi , \left ( a^2+1 \right ) \pi \right ] \left [ 2a \pi , \left ( a^2+1 \right ) \pi \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/b5871df3d5a1f9a3d9436dde0aba0a39.png) η εξίσωση έχει ακριβώς έξι διαφορετικές ρίζες.
η εξίσωση έχει ακριβώς έξι διαφορετικές ρίζες. παρατηρούμε ότι ήδη από την τιμή
παρατηρούμε ότι ήδη από την τιμή 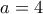 οι ρίζες είναι περισσότερες από έξι.
οι ρίζες είναι περισσότερες από έξι.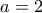 οι διαφορετικές ρίζες είναι μόλις
οι διαφορετικές ρίζες είναι μόλις  .
. στο διάστημα
στο διάστημα 
 η εξίσωση παρουσιάζει
η εξίσωση παρουσιάζει  διαφορετικές ρίζες στο αντίστοιχο διάστημα, ενώ για
διαφορετικές ρίζες στο αντίστοιχο διάστημα, ενώ για  η εξίσωση παρουσιάζει περισσότερες από έξι ρίζες.
η εξίσωση παρουσιάζει περισσότερες από έξι ρίζες.
 και
και 

 τότε
τότε  στο οποίο η εξίσωση έχει όντως έξι διαφορετικές ρίζες τις:
στο οποίο η εξίσωση έχει όντως έξι διαφορετικές ρίζες τις:

 υπάρχουν πέντε διαφορετικές λύσεις.
υπάρχουν πέντε διαφορετικές λύσεις. υπάρχουν ακριβώς έξι οι:
υπάρχουν ακριβώς έξι οι:
 , οι ίδιες με πριν.
, οι ίδιες με πριν. οι ρίζες αυξάνονται πάνω από το επιθυμητό.
οι ρίζες αυξάνονται πάνω από το επιθυμητό. είναι:
είναι:
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες