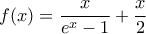
α) Βρείτε το πεδίο ορισμού της
 ............................................................... ΜΟΝΑΔΕΣ 5
............................................................... ΜΟΝΑΔΕΣ 5β) Βρείτε το
 .............................................................................. ΜΟΝΑΔΕΣ 6
.............................................................................. ΜΟΝΑΔΕΣ 6γ) Βρείτε το σημείο τομής της γραφικής παράστασης της
 με την ευθεία
με την ευθεία  ..... ΜΟΝΑΔΕΣ 6
..... ΜΟΝΑΔΕΣ 6δ) Δείξτε ότι η
 είναι άρτια ..................................................................... ΜΟΝΑΔΕΣ 8
είναι άρτια ..................................................................... ΜΟΝΑΔΕΣ 8Λήξης φραγής για τους μη μαθητές , η ώρα εκκίνησης της γιορτής του κ. Κ. Τηλέγραφου .

 , άρα
, άρα 

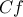 με την ευθεία
με την ευθεία 

 )
)  . Επομένως, πρόκειται για το σημείο έστω
. Επομένως, πρόκειται για το σημείο έστω  .
. το
το  και
και  το οποίο είναι το
το οποίο είναι το  , άρα η
, άρα η  άρτια.
άρτια.
 του Bernoulli, οι οποίοι έχουν πολλές εφαρμογές
του Bernoulli, οι οποίοι έχουν πολλές εφαρμογές .
.  είναι
είναι  . Βλέπε
. Βλέπε